Les deuxième et troisième lois de Newton

Fondamental :

La statique nous apprend que les forces internes d'un solide ou d'un fluide sont en équilibre avec les forces externes. Dans le cas d'un solide ou d'un fluide en mouvement, la seconde loi de Newton nous permet de lier la variation de la quantité de mouvement aux forces externes.

La deuxième loi de Newton permet donc d'intégrer le mouvement du fluide dans l'équilibre des forces. Ainsi la force exercée sur le fluide $F_{fluide}$ s'exprime :

$F_{fluide}=\frac{d(mv)}{dt}=ma$

Compte-tenu du fait que dans l'interaction fluide-structure nous nous intéressons à l'effort sur les parois solides, on met en application la troisième loi de Newton et la réaction $F$ sur le solide s'exprime en fonction de la variation de la quantité de mouvement du fluide :

$F = \frac{- d (m v)}{dt} = - m a$

$N = (kg\ m/s)/s = kg\ m/s^2$

Le fluide, par sa variation de quantité de mouvement, exerce une force sur les parois.

Si on considère un fluide incompressible et en charge, la masse et la densité étant constantes, seule la vitesse peut faire varier la quantité de mouvement, par sa variation en direction et/ou en grandeur.

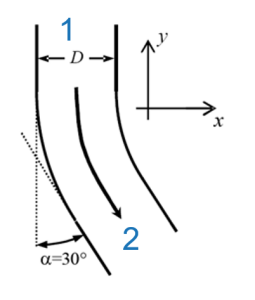
Écoulement dans un coude et réaction | Informations^[1]

L'étude de l'écoulement dans un tuyau fixe montre que la courbure dans le tuyau génère une réaction sur le tuyau selon la troisième loi de Newton.

$F_{x} = ρ Q (v_{x 1} - v_{x 2})$

C'est la courbure d'une ligne de courant ou filet fluide qui exerce une force d'inertie.

On observe que la force est dans le sens contraire de la variation vitesse. En généralisant :

$F_{i} = - ρ Q Δ v_{i}$

Fondamental : Application de la loi de Newton à un moulinet

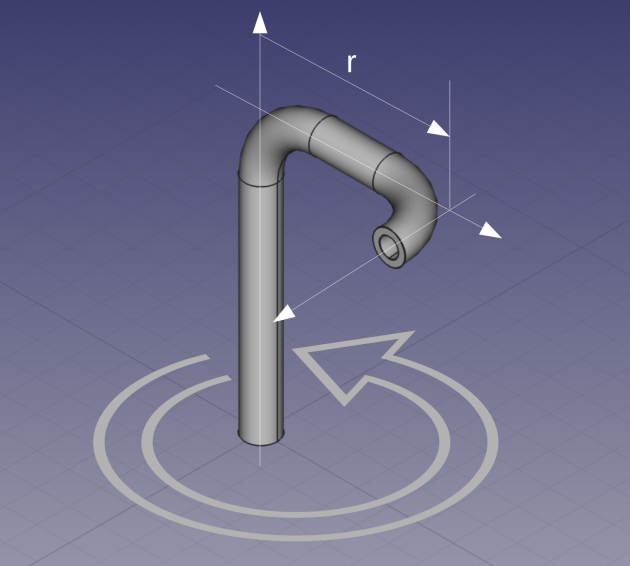
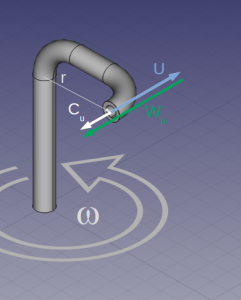
Le moulinet montré est alimenté en bas par un débit vertical et tourne à une vitesse constante. Le débit sort tangentiellement et horizontalement à une distance r de l'axe dans la direction opposée à la rotation.

Les équations décrivant ce phénomène sont :

L'équation de Newton : $F_{i} = - ρ Q Δ v_{i}$ où l'indice $i$ réfère à l'axe tangentiel. Dans cet axe, la vitesse du fluide est $C_u$ .

$\Delta v_i$ est la différence de vitesse tangentielle entre la sortie et l'entrée. À l'entrée, la vitesse tangentielle est nulle donc on notera $\Delta v_i = C_u$, la vitesse tangentielle à la sortie.

On calcule le couple moteur agissant sur le moulinet : $M = - ρ Q C_{u} \times r$

Puisque qu'il s'agit d'un moteur en rotation la puissance s'exprime : $P = M ω = - (ρ Q C_{u} \times r) * ω$

On note que pour une puissance positive, le couple et la vitesse angulaire doivent être dans le même sens.

En réarrangeant les termes de cette équation on identifie $\rho Q$ le débit massique tel que vu précédemment et le terme $C_u r \omega$ est l'énergie massique exprimée en $m^2/s^2$ ou de façon équivalente en $J/kg$ .

L'énergie massique que développe le moulinet peut donc se calculer à partir des vitesses tangentielles fluide et solide ainsi :

$E=-C_u r \ \omega=-C_uU$

Comme on l'a vu, la force résulte d'un changement de direction axiale, à l'entrée, vers une direction tangentielle, à la sortie. Cet effort crée un couple qui à cause de la vitesse angulaire donne une puissance. Cette puissance est en fait le produit d'un débit massique par une énergie massique .

On observe que l'expression de l'énergie massique est le produit de la vitesse tangentielle fluide par la vitesse tangentielle solide. Ces deux vitesses étant dans des sens opposés.

Exemple : Vitesse relative et vitesse absolue

Exemple 1

Supposons un moulinet tel qu'illustré avec :

une vitesse débitante ($W_u$) à la sortie du moulinet égale à $-10 m/s$,
cette sortie se trouve à 1 m de l'axe de rotation, c'est le rayon ($r$) de la sortie,
une vitesse angulaire ($\omega$) de 10 rad/s.

Vitesses à la sortie du moulinet | Informations^[3]

La vitesse tangentielle du moulinet à la sortie se calcule : $U = r \times \omega = 10 \ m/s$

La vitesse débitante ($W_u$) est une vitesse relative au moulinet qui est en rotation telle que : $C_u = U+W_u$ .

$U$ et $W_u$ étant égales mais de sens inverse, le $C_u$ est nul et donc la puissance générée est nulle.

Pour avoir une puissance positive, il faut une ou une combinaison des possibilités suivantes :

Réduire la vitesse angulaire.
Réduire le rayon de sortie.
Diminuer la section de passage à la sortie pour augmenter la vitesse du fluide à la sortie.
Augmenter le débit.

On réalise qu'avec l'inverse de ces possibilités, on obtiendra une puissance négative, c'est-à-dire qu'il faudra un moteur pour faire tourner le moulinet.

Exemple 2

Reprenons maintenant le calcul avec les mêmes données sauf :

une vitesse débitante ($W_u$) à la sortie du moulinet égale à $-20 \ m/s$ et qui correspond à un débit de $1 \ m³/s$.

La vitesse tangentielle du moulinet à la sortie reste à $10 \ m/s$

$C_u = U+W_u$ et donc $C_u=(10-20)m/s = -10 \ m/s$

La force exercée sera de $F_{i} = - ρ Q Δ v_{i}$ $=-1000*1*-10=10000 \ N$

La puissance produite sera $P = M ω = - (ρ Q C_{u} \times r) * ω$ $=-(1000*1*-10*1)*10=100000 \ W=100\ kW$