Générer des profils hydrauliques en deux dimensions

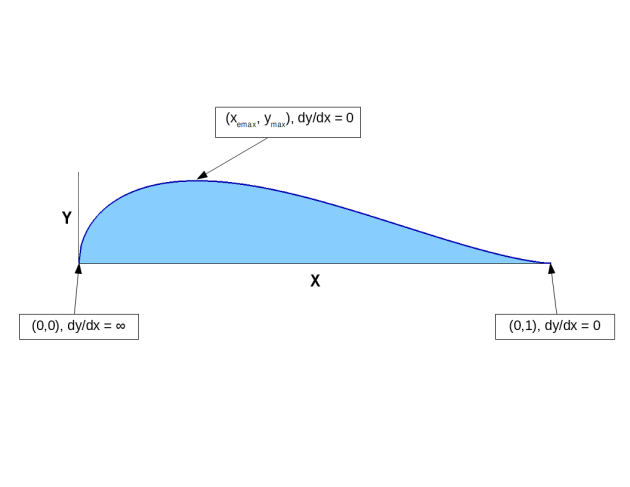
Générer des profils hydrauliques en deux dimensions - Théorie

Un profil de base - Les critères

La génération d'un profil hydraulique par une équation algébrique peut être considérée comme un point de départ pour une conception.

Imposons que sa forme canonique soit pour une longueur de 1 ou plus précisément une corde^[1] de longueur 1.

Le profil doit satisfaire les critères suivant :

Au bord d'attaque, x=0 , dy/dx = ∞.
Au bord de fuite, x=1, dy/dx = 0.
À l'épaisseur maximale, x = x_emax, y = y_max et dy/dx = 0.

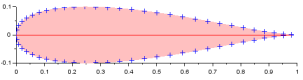
On observe qu'ainsi, on obtient un demi profil. Le profil complet est donc l'assemblage de deux demis profils qui peuvent être différenciés mais de même longueur.

Les propriétés d'un profil hydraulique | Informations^[2]

Dans les prochaines lignes nous allons voir comment créer des profils avec toute la latitude nécessaire en conception de turbine hydraulique.

La première méthode fait appel aux logiciels de conception assistée par ordinateur (CAO ou CAD) comme FreeCAD où les formes à pôles sont intégrés et donnent une méthode robuste et flexible au concepteur.

Ensuite. on y présente 2 modèles algébriques :

La courbe en oignon.
Le polynôme.

qui peuvent être programmé aisément. À titre d'exemple, un programme en Scilab est fourni.

Fondamental : Traçage d'un profil hydraulique en deux dimensions dans un logiciel de conception assisté par ordinateur

De nos jours, tous les systèmes de CAO, font appel aux formes à pôle pour générer les géométries complexes. Ces formes sont des implantations des courbes de Bézier, des Bsplines et des Nurbs, ces dernières étant la généralisation de toutes les autres avec encore plus de possibilités. Pour la théorie de ces formes on pourra se référer à Wikipedia ainsi : NURBS , Bézier.

La mise en place de la méthode de génération d'un profil en deux dimensions avec FreeCAD est ici .

Fondamental : De la courbe en oignon de base à la courbe en oignon paramétrée

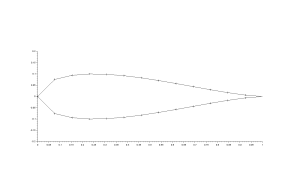
La recherche d'une fonction algébrique qui satisfait les critères a amené le professeur Th. Bovet^[3] à proposer la courbe en oignon (Zwiebelkurve) ou oignoïde qui s'exprime dans sa forme simplifiée pour x variant entre 0 et 1 comme :

\begin{matrix} y = 2 \sqrt{x {(1 - x)}^{3}} \\ avec comme dérivée: \\ \frac{dy}{dx} = \frac{(1 + x (- 6 + x (9 - 4 x)))}{\sqrt{x {(1 - x)}^{3}}} \end{matrix}

On peut donc extraire certaines valeurs caractéristiques de cette oignoïde.

Le maximum de l'épaisseur se trouve lorsque dy/dx = 0 avec une des racine à x = x_emax= 0,25 ; ceci correspond à une demie épaisseur maximale de y = y_max = $\frac{3 \sqrt{3}}{8}$ .

La valeur de l'épaisseur maximale et sa position ont avantage à être flexibles.

Donc, si on veut imposer une demie épaisseur relative maximale y_max on obtient l'équation de l'oignon suivante :

y = \frac{16 \sqrt{(3)}}{9} * y_{\max} * \sqrt{x {(1 - x)}^{3}}

Maintenant, sur le segment x entre 0 et un on trouve le maximum d'épaisseur à 0,25. Pour déplacer ce point à un endroit spécifique, il faut faire une transformation de la variable faisant correspondre :

x	x_t
0	0
0,25	x_emax
1	1

Supposons une fonction du type exponentielle pour cette transformation.

\begin{matrix} x = x_{t}^{p} \\ ainsi pour la position 0,25 on aura : \\ 0,25 = x_{t}^{p} \\ ce qui implique que : \\ p = \log_{x} 0,25 = (\frac{\log 0,25}{\log x_{emax}}) \\ et donc : \\ x = x_{t}^{(\frac{\log 0,25}{\log x_{emax}})} \end{matrix}

Il suffit de placer cette transformation de variable dans la courbe oignon pour obtenir la courbe en oignon paramétrée :

y = \frac{16 \sqrt{(3)}}{9} * y_{\max} * \sqrt{x_{t}^{(\frac{\log 0,25}{\log x_{emax}})} {(1 - x_{t}^{(\frac{\log 0,25}{\log x_{emax}})})}^{3}}

Oignon1 — Différentes possibilités de la courbe en oignon

Oignon2 — Différentes possibilités de la courbe en oignon

Fondamental : Une courbe polynomiale

Pour ce modèle algébrique on exprime la courbe comme étant une fonction de l'abscisse curviligne variant entre 0 et 1. On exprime donc les coordonnées (x,y) comme étant fonctions d'une même variable t, l'abscisse curviligne. Donc x=f(t) et y=f(t).

Pour x, aux conditions numérotées 1,3 et 4 ci-bas et qui correspondent aux critères, on ajoute une quatrième condition qui est la position sur l'abscisse curviligne de l'épaisseur du profil. Donc à t=u, correspond x_u et y_u., doit la condition numérotée 7. Ceci nous amène donc à 4 variables qui commandent une fonction cubique.

Parallèlement, pour y on identifie donc 5 conditions numérotées 2, 5 ,6, 8 et 9 qui commandent un polynôme quartique.

\begin{matrix} Soit x et y des fonctions de t \\ x = f (t) = f_{0} + f_{1} t + f_{2} t^{2} + f_{3} t^{3} \\ y = g (t) = g_{0} + g_{1} t + g_{2} t^{2} + g_{3} t^{3} + g_{4} t^{4} \\ \frac{dx}{dt} = f_{1} + 2 f_{2} t + 3 f_{3} t^{2} \\ \frac{dy}{dt} = g_{1} + 2 g_{2} t + 3 g_{3} t^{2} + 4 g_{4} t^{3} \\ \frac{d^{2} y}{{dt}^{2}} = 2 g_{2} + 6 g_{3} t + 12 g_{4} t^{2} \\ Conditions à t=0 : \\ (1) x = 0 \\ (2) y = 0 \\ (3) \frac{dx}{dy} = \frac{dx}{dt} = 0 \\ (1) \to f_{0} = 0 \\ (2) \to g_{o} = 0 \\ (3) \to f_{1} = 0 \\ Conditions à t=1 : \\ (4) x = 1 \\ (5) y = 0 \\ (6) \frac{dy}{dx} = \frac{dy}{dt} = 0 \\ (4) \to f_{2} + f_{3} = 1 \\ (5) \to g_{1} + g_{2} + g_{3} + g_{4} = 0 \\ (6) \to g_{1} + 2 g_{2} + 3 g_{3} + 4 g_{4} = 0 \\ Conditions à t=u : \\ (7) x = x_{u} \\ (8) y = y_{u} \\ (9) \frac{dy}{dx} = \frac{dy}{dt} = 0 \\ (7) \to f_{2} u^{2} + f_{3} u^{3} = x_{u} \\ (8) \to g_{1} u + g_{2} u^{2} + g_{3} u^{3} + g_{4} u^{4} = y_{u} \\ (9) \to g_{1} + 2 g_{2} u + 3 g_{3} u^{2} + 4 g_{4} u^{3} = 0 \\ Solutionnons pour g4 et u \\ (5) & (6) \to g_{2} + 2 g_{3} + 3 g_{4} = 0 \\ g_{2} = - 2 g_{3} - 3 g_{4} \\ g_{1} = g_{3} + 2 g_{4} \\ (8) \to (g_{3} + 2 g_{4}) u + (- 2 g_{3} - 3 g_{4}) u^{2} + g_{3} u^{3} + g_{4} u^{4} = y_{u} \\ g_{3} (u - 2 u^{2} + u^{3}) + g_{4} (2 u - 3 u^{2} + u^{4}) = y_{u} \\ g_{3} = \frac{y_{u} - g_{4} (2 u - 3 u^{2} + u^{4})}{(u - 2 u^{2} + u^{3})} \\ g_{3} = \frac{y_{u}}{(u - 2 u^{2} + u^{3})} - g_{4} \frac{2 u - 3 u^{2} + u^{4}}{u - 2 u^{2} + u^{3}} \\ (9) \to g_{3} + 2 g_{4} + 2 (- 2 g_{3} - 3 g_{4}) u + 3 g_{3} u^{2} + 4 g_{4} u^{3} = 0 \\ g_{3} (1 - 4 u + 3 u^{2}) + g_{4} (2 - 6 u + 4 u^{3}) = 0 \\ (\frac{y_{u}}{(u - 2 u^{2} + u^{3})} - g_{4} \frac{2 u - 3 u^{2} + u^{4}}{u - 2 u^{2} + u^{3}}) (1 - 4 u + 3 u^{2}) + g_{4} (2 - 6 u + 4 u^{3}) = 0 \\ g_{4} = \frac{\frac{- y_{u} (1 - 4 u + 3 u^{2})}{(u - 2 u^{2} + u^{3})}}{(2 - 6 u + 4 u^{3}) - (1 - 4 u + 3 u^{2}) \frac{2 u - 3 u^{2} + u^{4}}{u - 2 u^{2} + u^{3}}} \end{matrix}

Ce modèle comparé à la courbe en oignon donne un peu plus de flexibilité sur la courbe tout en respectant les critères. Ce plus la distribution des points est plus optimale et permet d'éviter d'ajouter un facteur de concentration comme pour la courbe en oignon.

Poly1 — Le modèle polynomial montre beaucoup de flexibilité

Poly2 — Le modèle polynomial montre beaucoup de flexibilité

Complément : Génération des points sur le profil

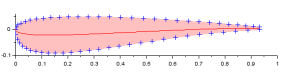
Les besoins d'affichage, de calcul numérique et de transmission à un modeleur géométrique créent le besoin de discrétisation du profil. Or, on s'aperçoit rapidement qu'une génération des points à partir de coordonnées x régulières crée une qualité de profil qui se dégrade au bord d'attaque en présentant des angles plus on moins acceptables selon le nombre de points utilisé pour représenter le profil. Augmenter le nombre de points peut être une solution.

À cause de la courbure au bord d'attaque la définition régulière en x n'est pas satisfaisante | Informations^[4]

Une première étape pour une solution plus élégante est de définir les points à égale distance sur le profil donc sur l'abscisse curviligne du profil.

\begin{matrix} s (t) = \int_{0}^{t} \sqrt{{(\frac{dx}{dt})}^{2} + {(\frac{dy}{dt})}^{2}} dt \\ qui se met en place numériquement en associant à chaque intervalle i \to i + 1 : la distance s_{i} \\ s_{i} = \sqrt{({(Δ x_{i})}^{2} + {(Δ y_{i})}^{2})} \\ dont la sommation donne la longueur totale \\ longueur = \sum s_{i} \\ on peut donc associer une abscisse curviligne t de longeur totale 1 : \\ t_{i} = t_{(i - 1)} + s_{(i - 1)} / longueur \end{matrix}

Dès lors, on peut calculer à l'aide d'un interpolateur toute coordonnée x ou y comme une fonction de t, l'abscisse curviligne qui varie entre 0 et 1 le long de la courbe.

Le résultat d'une distribution à égale distance le long du profil curviligne améliore la définition.

La distribution régulière en abscisse curviligne améliore la définition du profil | Informations^[5]

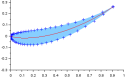
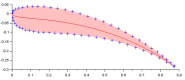
Ce résultat demeure perfectible et se corrige en introduisant la notion de concentration des points au bord d'attaque. Si on exprime que la longueur d'un intervalle est une proportion (c) de l'intervalle précédent.

Donc pour n points et n-1 intervalles, on peut écrire pour un premier intervalle Δd :

\begin{matrix} d_{1} = Δ d \\ d_{i} = c d_{(i - 1)} \\ d_{total} = d_{1} + d_{2} + d_{3} + ... d_{(n - 2)} + d_{(n - 1)} \\ d_{total} = Δ d + c Δ d + c^{2} Δ d + c^{3} Δ d + ... + c^{(n - 3)} Δ d + c^{(n - 2)} Δ d \\ d_{total} = Δ d (1 + c + c^{2} + ... + c^{(n - 2)}) \\ en normalisant pour une longueur curviligne totale de 1 et posant Δ d = 1 \\ 1 = \frac{Δ d}{d_{total}} (1 + c + c^{2} + ... + c^{(n - 2)}) = \frac{1}{d_{total}} (1 + c + c^{2} + ... + c^{(n - 2)}) \\ En reconstruidant la position curviligne des points compris entre 0 et 1: \\ 1 = s_{0} + s_{1} + s_{2} + s_{3} + ... s_{(n - 1)} + s_{n} \\ 1 = 0 + 1 / d_{total} + c / d_{total} + c^{2} / d_{total} ... \end{matrix}

On peut donc maintenant exprimer une distribution de points en fonction du facteur c. Pour un facteur c de 1,2 on obtient la distribution représentée sur la figure.

Distribution géométrique par une facteur de concentration | Informations^[6]

Complément : L'inscription du profil sur un arc de cercle

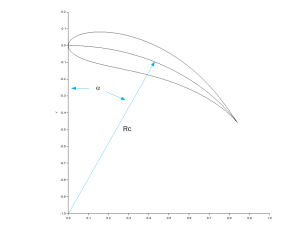
Pour donner une degré de liberté additionnel au concepteur, il est intéressant d'enrouler le profil généré en inscrivant la corde du profil sur une abscisse curviligne.

Le besoin est de dévier l'écoulement d'un certain angle. L'arc de cercle permet d'y arriver de façon graduelle et en douceur.

On veut donc inscrire le profil sur un arc de cercle.

Posons le bord d'attaque à la coordonnée (0, 0) et le centre du rayon de courbure est situé à (0,-Rc) où Rc est le rayon de courbure.

Le rayon d'un point sur le profil sera :

Enroulement du profil sur le rayon de courbure Rc | Informations^[7]

\begin{matrix} {Rc}_{i} = Rc + y_{i} \\ La positi0n angulaire de ce point sera : \\ α_{i} = x_{x} / Rc \\ Les coordonnées cartésiennes sur le cercle de rayon Rc seront maintenant : \\ x_{i} = {Rc}_{i} * \sin (α_{i}) \\ y_{i} = {Rc}_{i} * \cos (α_{i}) - Rc \end{matrix}

Étude du squelette d'un profil en 2D

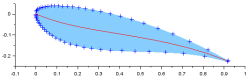
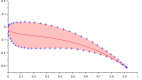
Un profil complet est un assemblage d'une face intrados et d'une face extrados. Chacune des deux faces du profil peut être construite avec une épaisseurs maximale différenciée. Ci-contre, les deux profils intrados et extrados et la corde entre le bord d'attaque et le bord de fuite.

Profils avec épaisseurs différenciées en intrados et extrados et la corde | Informations^[8]

Les profils peuvent aussi s'inscrire sur une abscisse curviligne. Comme le profil peut ne pas être symétrique, le résultat est que le squelette ou la fibre neutre du profil n'est pas sur la corde.

Avec une loi d'épaisseur différenciée, le squelette s'incurve même si la corde reste parfaitement horizontale. — Le squelette permet de visualiser la déviation potentielle du fluide par le profil

Avec loi d'épaisseur différenciée et les profil inscrits sur un arc de cercle, on peut obtenir un squelette en "S". — Le squelette permet de visualiser la déviation potentielle du fluide par le profil

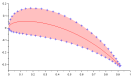
Le squelette est donc défini comme étant la moyenne des profils intrados et extrados. Il présente un angle amont au bord d'attaque et un angle aval au bord de fuite dont la différence nous donne la déviation potentielle.

Le squelette devient une indication importante du potentiel de déviation du fluide par le profil. C'est en fait un critère de conception.

Avec les paramètres d'épaisseur maximale des profils intrados et extrados et le rayon de courbure , on peut créer une large gamme de profils.

Complément :

La mise en place de la méthode de génération d'un profil en deux dimensions est ici .