Méthodes d'interpolation sur une colline
De la mesure à la représentation mathématique
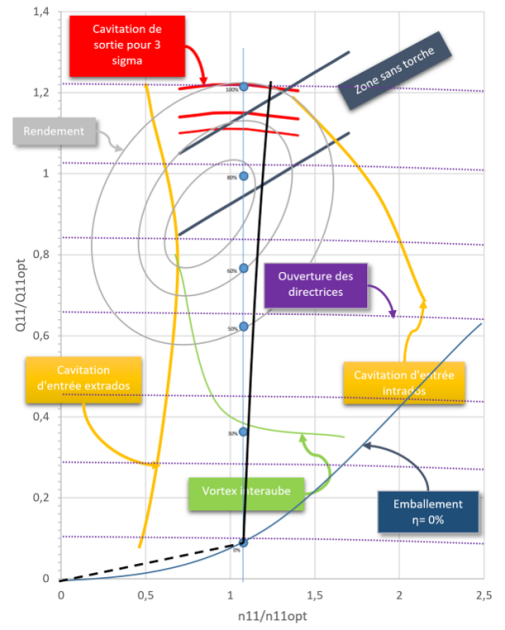
La colline de rendement est une représentation graphique de la performance de la turbine. Un présentation du fonctionnement de la turbine se trouve ici. Habituellement, la colline s'appuie sur 2 axes liés au débit et à la chute pour représenter sur une troisième dimension certaines valeurs qui peuvent être le rendement, la puissance, des limites liées à des phénomènes physique comme la cavitation, la torche, les vortex de charge partielle ou tout simplement les limites d'opération prévues par l'exploitant.
Ces données sont obtenues soit expérimentalement soit par calcul ou un mélange empirique de ces deux méthodes. Les données sont ponctuelles et habituellement distribuées irrégulièrement dans le domaine.
Entre les points de mesure, il peut être nécessaire de connaître les valeurs. Par exemple, on veut connaître le rendement à une puissance précise pour une raison contractuelle, ou on veut simuler un phénomène transitoire qui, par pas de temps, nous amène à des combinaisons de chute, vitesse de rotation et débit entre les points mesurés.
Pour prédire la performance entre les points mesurés, la solution la plus simple est l'interpolation. On pourrait aussi imaginer une modélisation de la physique mais la complexité d'une telle mise en œuvre la rend souvent inaccessible.
Remarque : Les paramètres de l'interpolation.
Le plus souvent l'hydraulicien a deux besoins qui s'expriment dans deux plans de travail différents ; chaque plan est défini par le choix des variables en abscisse et en ordonnée :
Le plan performance : il s'agit de présenter les performances dans un plan chute-débit ou chute-puissance pour fin de comparaison.
En x, la chute peut être remplacée par la combinaison, vitesse de rotation et chute, utilisée pour calculer le chiffre de similitude[2] choisi soit : le facteur de vitesse (nED, n11, Ku, ωED) ou coefficient d'énergie (EnD, psi, EωD). Une valeur normalisée de ces facteurs ou coefficients peut aussi être utilisée .
En y, le débit ou la puissance peuvent être remplacés par le chiffre de similitude[3] les représentant : le facteur de débit (QED, Q11 ou Kcm) ou coefficient de débit (QnD, φ ou QωD) ou le facteur de puissance (PED, P11 ou KP) ou coefficient de puissance (PnD, λ ou PωD). Une valeur normalisée de ces facteur ou coefficients peut aussi être utilisée.
Le plan opération : il s'agit de prédire le comportement de la turbine dans un plan d'opération chute-ouverture :
En x, comme ci-haut, la combinaison, vitesse de rotation et chute, utilisée pour calculer le chiffre de similitude[4] choisi soit : le facteur de vitesse (nED, n11, Ku, ωED) ou coefficient d'énergie (EnD, psi, EωD).
En y, la configuration géométrique caractérisée :
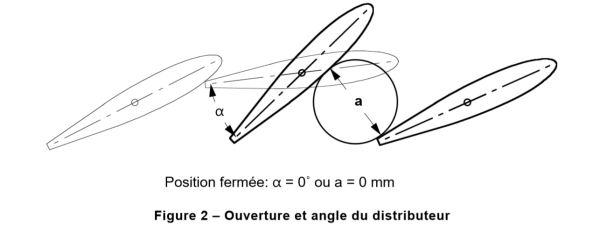
Par l'angle de l'ouverture du distributeur ou
Par la valeur de l'ouverture en mm comme présenté sur cette figure du CEI.
L'opération d'une turbine passe par une commande de l'ouverture en vue d'obtenir le point d'opération souhaité. À la valeur de l'ouverture correspond une position dans la course du servomoteur. La relation entre les deux est strictement géométrique et particulière à la réalisation du prototype[5].
À l'origine, l'information est collectée dans le plan d'opération en positionnant l'ouverture des directrices et pour un chiffre de similitude liée à la vitesse ; on associe à ce couple de valeurs une troisième valeur qui peut être un chiffre représentant le débit, la puissance, le rendement, etc. En clair, on a pour chaque x et y, plusieurs z associés. Il s'agit donc de représentations de plusieurs surfaces liées au même plan.
Exemple : Exemple d'une colline numérique
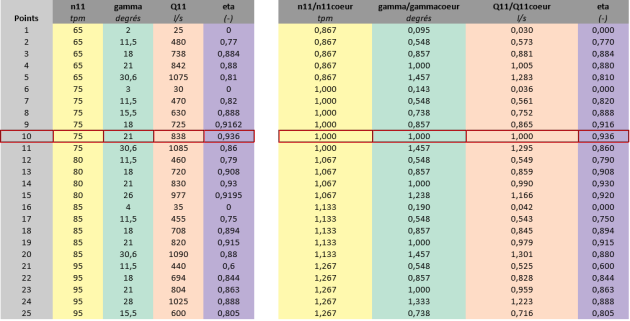
Par exemple, une colline pourrait être décrite par les valeurs suivantes :
Le numéro du point
La valeur n11 correspondant à l'abscisse
L'ouverture des directrices présentée comme étant l'angle α.
La valeur Q11 qui est le chiffre de débit
La valeur η représentant le rendement
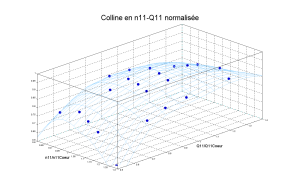
La mathématique de l'interpolation est très influencée par les proportions du domaine d'interpolation. L'idéal est que ce domaine se rapproche de la forme du cube. Une pratique courante est de diviser la coordonnée par sa valeur au sommet de rendement. Sur le tableau précédent, le sommet est encadré en rouge. Ainsi, la coordonnée (x,y) du sommet de rendement est (1,1).
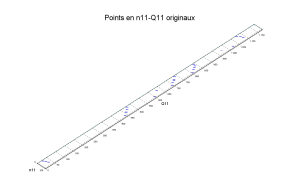
Sur cette figure on voit bien la disproportion des dimensions x et y du domaine d'interpolation. Le résultat de l'interpolation sera de moins bonne qualité.
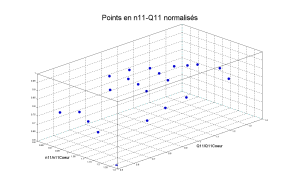
Ici, on a utilisé les coordonnées normalisées. Les proportions du domaine sont vraiment plus agréable à l’œil et à l'interpolateur. Il s'agit pourtant des mêmes données d'essai.
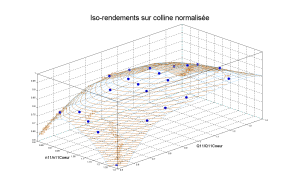
L'interpolateur construit une représentation analytique des valeurs dans tout le domaine. Cette représentation passe obligatoirement par les points de la colline
Ici, on représente les iso-rendements tel que calculés par l'interpolateur.
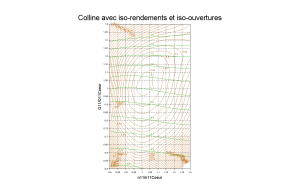
Par une vue en plan, on obtient la colline classique. Comme pour les iso-rendements, les iso-ouvertures sont obtenues par leur propre représentation analytique et donc leur propre interpolateur.
Remarque :
Une difficulté importante pour l'interpolation sur une colline vient de la distribution irrégulière des données.
Fondamental : Interpolation sur des données distribuées irrégulièrement
Une méthode mathématique pour interpoler sur des données distribuées irrégulièrement est l' Algorithm 790: CSHEP2D: Cubic Shepard method for bivariate interpolation of scattered data[13] qui a été publié à l'ACM (Association for Computing Machinery en 1999. Elle fait partie maintenant de la bibliothèque de Scilab. Malgré la difficulté du traitement mathématique, son utilisation est assez simple.
Son principe se base sur la génération d'une surface bicubique dont les coefficients sont influencés par la distance au points voisins.
Cette surface est continue jusqu'à la deuxième dérivée.
Dans une première étape, on calcule les coefficients d'interpolation avec la fonction cshep2d puis on calcule la valeur qu'on désire interpoler en spécifiant ses coordonnées x et y à l'aide de la fonction eval_cshep2d.
Comme pour toute fonction mathématique, il faut s'assurer qu'à chaque combinaison de x et y corresponde une seule valeur de z.
On ne peut cumuler plusieurs lectures à un point de fonctionnement et les donner à l'interpolateur. Il faut traiter ces lectures pour obtenir un seul point pour l'interpolateur.
Sans être régulière, la densité la plus uniforme possible des points est garante d'une meilleure précision.
L'extrapolation en dehors de la région des données est évidemment à éviter.
Cet algorithme de calcul est très efficace et donne des collines précises et lisses.
À partir d'une telle colline, il est possible de générer une grille régulière qui sera utilisée par le tableur pour interpoler linéairement.
Fondamental : Interpolation sur des données distribuées régulièrement
Il existe pour les tableurs Excel et Calc une même fonction d'interpolation linéaire interpo2
pour Calc Interpo2 du site https://extensions.libreoffice.org/extensions/interpolation-for-calc et
pour Excel Interpo2 du site https://personales.gestion.unican.es/martinji/Interpolation.htm
qui permet d'interpoler sur une colline facilement dans une feuille de calcul. Pour l'activer, il faut lui donner accès à une grille régulière qui peut être avantageusement obtenue avec l'algorithme présenté au paragraphe précédent.
Simulation : Interpolation pour un point de fonctionnement
On présente ici une mise en situation simple pour expliquer le fonctionnement de l'interpolation sur des données éparpillées.
L'ensemble des outils d'interpolation sont dans l'archive compressée Interpolation.zip qu'on trouve à https://michelsabourin.scenari-community.org/Outils . Il faut suivre les instructions d'installation dans le fichier Lisez-moi.txt.
Les données de la colline, tel que présentées plus haut dans l'exemple, sont dans le fichier colline_exemple.xls. Ce fichier doit obligatoirement correspondre à la version Excel 97-2013. Il faut donc le sauvegarder sous cette version.
Il faut respecter l'ordre et le contenu des colonnes. Ce qui est montré dans l'exemple se trouve à l'onglet 2. C'est l'onglet 1 qui contient les données nécessaires qui correspondent en fait, aux données de la colline normalisée, sans l'entête et le numéro des points et positionné à la ligne 1 et la colonne 1. Cet onglet ne doit contenir que les données de la colline, aucun graphique n'est permis.
Le script Scilab s'appelle CollinePoint.sce. Il permet d'interpoler un point à la fois sur la colline. La colline est normalisée à l'interne pour le calcul, il n'est pas nécessaire de le faire à dans le fichier colline.
On doit d'abord indiquer si on travaille dans le plan de performance style ned-Qed ou dans le plan d'opération style ned-Ouverture.
Puis, on entre dans les cases appropriées les valeurs x et y où on veut connaître le rendement.
On peut en boucle donner une série de points.
Il s'agit ici d'un démonstrateur et le code fourni montre comment manipuler les fonctions cshep2d et eval_cshep2d.
Simulation : Traçage d'une colline pour analyse
Le script CollineGrille.sce permet de représenter graphiquement la colline, de générer des collines sur des grilles régulières et d'interpoler des séries de points grâce à une interface usager conviviale. Un série de point peut par exemple représenter une prise de charge à la chute nominale.
Alors que le script précédent, sur l'interpolation à un point, travaille à l'aveuglette, celui-ci est agrémenté d'un graphique qui permet d'apprécier en trois dimensions le domaine de fonctionnement de la turbine.
Son interface est intuitive et le script s'appuie sur la même définition du fichier colline décrite plus haut.
L'interface se divisent en deux parties .Les commandes de la partie gauche concernent le calcul. Celles de la partie droite concerne l'habillage graphique.
Partie gauche de l'interface :
Lors du lancement, on demande la lecture du fichier colline ; l'interface comporte aussi un bouton pour lire une autre colline et relancer le processus d'analyse. Il n'est pas nécessaire que la colline soit normalisée dans le fichier. Le programme la normalise à l'interne pour le calcul.
L'interpolation se fait soit dans le plan d'analyse de performance (ned-Qed) ou dans le plan d'opération (ned-Ouv), il s'agit d'activer le bouton y correspondant.
Les limites du domaine représenté peuvent être ajustée. Cela se fait en conservant les mêmes coefficients d'interpolation. Les pas de l'interpolation n'affectent que la représentation graphique. Après les modifications des valeurs, s'assurer de relancer le calcul en appuyant sur le bouton "Traçage avec les nouvelles limites du domaine et pas de la grille".
On a le choix de 4 types de vue. Soient les vues en plan, en élévation, de profil ou isométrique activable par leur bouton.
Tous ces choix sont sauvegardées dans le fichier de session situé dans le répertoire de la colline lueé avec comme nom, celui de la colline mais avec l'extension .dat.
Partie droite de l'interface :
On peut modifier les écritures des titres et axes qu'on active en appuyant sur le bouton "Modification des écritures".
La visibilité, la couleur et la largeur de trait des objets graphiques sont ajustables.
La colline est définie par une suite de points dans un fichier .xls. Chaque point est une ligne de quatre colonnes :
Chiffre de vitesse
Ouverture
Chiffre de débit
Rendement
Il ne faut pas que le fichier .xls contienne d'autres informations.
Le nombre de ligne correspond au nombre de point. On peut vérifier la colline lue avec le bouton Vérifier la colline lue.
Les séries de points à interpoler sur la colline sont dans un fichier .xls. Il y a une série de points par feuille du fichier. Il ne peut y avoir plus de 5 feuilles. La lecture s'active par le bouton.
Le format de la série de points est pour chaque ligne la coordonnée x en colonne 1 et la coordonnée y en colonne 2.
Lors de la lecture, le type de colline actif (ned-Qed ou ned-Ouv) définit l'abscisse (colonne1) et l'ordonnée (colonne 2) et ainsi l'interpolation à effectuer. Dès la lecture l'interpolation s'effectue. On peut aussi constater le résultat en appuyant sur le bouton "Vérifier les points".
Le résultat est affiché automatiquement sur le graphique et les collines quadrillées régulièrement sont générées.
Si l'interpolation de la colline a été sélectionnée pour se faire dans le plan d'analyse de la performance de la performance (ned-Qed) les deux collines générées sur des grilles rectangulaires sont :
celle en rendement fonction de ned et Qed et
celle en ouverture fonction de ned et Qed.
Si par contre, l'interpolation a été sélectionnée pour se faire dans le plan d'opération (ned-Ouv), les deux collines générées sont :
celle en rendement fonction de ned et Ouv et
celle en ouverture fonction de ned et Ouv.
Les boutons d'habillage sont ajoutés selon les choix.
Les colline quadrillées régulièrement sont automatiquement sauvegardées dans des fichiers .csv du nom de la colline d'origine associé avec le mot Rendement, Debit ou Ouverture suivant le type de colline choisi.
Un fichier .csv contenant le résultat de l'interpolation est créé pour chaque série dans le même format que celui du fichier colline. Le nom du fichier .csv est l'agrégat du nom du fichier des séries avec le nom de la feuille.
Les fichiers .xls fournis dans l'archive (Interpolation.zip qu'on trouve à https://michelsabourin.scenari-community.org/Outils) permettent de tester le script. On y trouve les fichier Colline_exemple.xls et Series_exemple.xls qui contiennent une colline et des séries de points à interpoler.
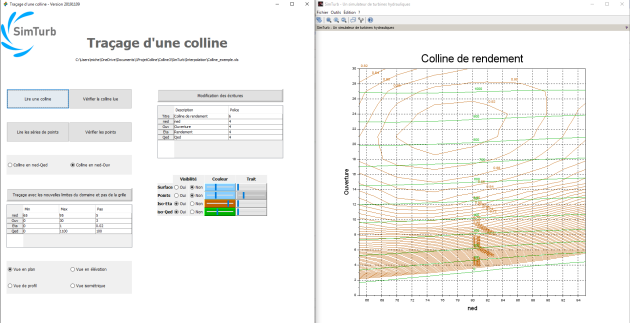
La figure suivante présente l'interface et le résultat graphique de ce script.
Conseil : Sommaire - Conseils pour interpoler sur une colline
Essentiellement, il faut disposer d'une colline numérique ; donc créer un fichier .xls qui contient l'information.
Cela se fait à partir de Calc de LibreOffice ou Excel de Microsoft. Dans les 2 cas, il faut s'assurer de sauvegarder en mentionnant le type .xls , soit celui de Classeur Excel 97-2003 (*.xls).
L'information doit être dans le premier onglet, celui le plus à gauche de la liste. Dans cette feuille, il ne doit pas y avoir d'autre information ni graphique.
Selon l'information disponible, les résultats numériques de la mesure transposés à un Reynolds unique seront les plus précises. Il faut choisir des points à peu près à égale distance les uns des autres. La notion de distance ici est très subjective mais basée sur l'apparence du graphique, elle correspond assez bien à un idéal d'interpolation.
Si l'information dont on dispose est graphique, il faudra prendre quelque dispositions additionnelles pour s'assurer d'une représentation globale suffisamment précise. Ainsi, il faut s'assurer de la régularité des iso-contours que ce soit ceux du rendement, ceux des ouvertures ou ceux du débit. Pour cela le script CollineGrille.sce est l'outil idéal. Il faut dans un premier temps s'assurer que le pas de la grille soit suffisamment fin pour les coordonnées x et y. Ensuite, en fonction de l'allure des iso-contours corriger les erreurs de lecture et ajouter des points aux endroits qui manquent de définition.
Une fois que les données donnent un résultat satisfaisant dans la zone à exploiter, on peut utiliser CollinePoint.sce ou une variation pour faire l'interpolation exactement où on veut. Ces deux programmes présentent exactement le même traitement numérique des données de la colline et de ce fait donne le même résultat.
Une autre option est de récupérer les données interpolées sur la surface quadrillée qui ont sauvegardées dans les fichiers .csv et de les incorporer dans une feuille de calcul pour être ensuite utilisé par la fonction d'interpolation linéaire Interpo2 . Il faut réaliser que la précision de cette interpolation dépend de la finesse de la grille générée par le script CollineGrille.sce.