Énergie locale et aux bornes
Définition : L'énergie massique locale et la différence d'énergie aux bornes d'un composant.
On appelle énergie totale \(E_i\) , l'énergie calculée par Bernoulli à une section i du circuit hydraulique.
\(E_{i} = {p_i \over \rho} + g z_i + {{v_i}^2 \over 2 }\)
Il s'agit d'une énergie massique, c'est à dire une énergie par unité de masse, soit des J/kg ce qui est équivalent à des m²/s² ou des Pa-m³/kg.
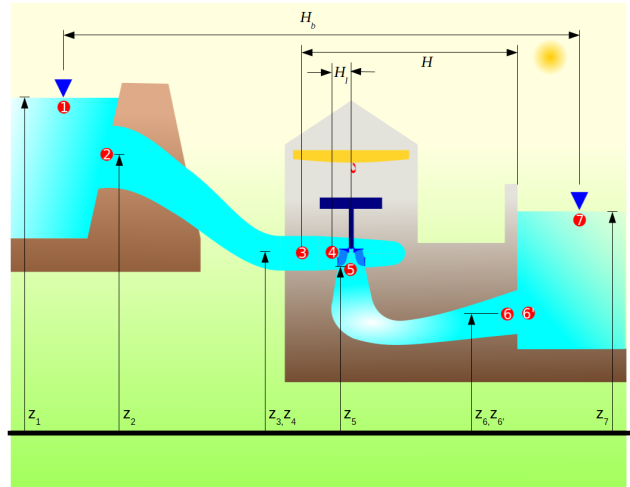
La perte de charge est une différence d'énergie massique perdue dans un composant. Par exemple, à la sortie de l'aspirateur, entre les points 6 et 6', l'énergie cinétique \({v_6^2 \over 2}\) est perdue et constitue une perte de charge.
L'énergie interne \(E_I\) est l'énergie aux bornes de la roue qui est transformée totalement en énergie mécanique à l'arbre. Elle se calcule avec Euler : \(E_I=gH_I=U_4C_{u4}-U_5C_{u5}\).
L'énergie nette \(E\) est l'énergie aux bornes de la turbines. Elle s'exprime comme étant \(E_{3} - E_{6}\). Toutefois, les énergies cinétiques en 3 et 6 sont calculées par rapport à leur vitesse moyenne ou vitesse débitante à la section considérée et exprimée par \(v_{moy} = {Q \over A}\).
L'énergie brute est l'énergie disponible au site, elle est liée aux niveaux amont et aval et de ce fait se calcule ainsi : \(E_b= (g z_1 + {p_{atm1} \over \rho})-(g z_7+{p_{atm7}\over \rho})\) .
En ingénierie hydraulique, on a tendance, par abus de langage, à parler d'énergie en terme de chute, il faut savoir que \(H ={ E \over g}\) et s'exprime en mce[1], ce qui est une représentation plus intuitive ou palpable de l'énergie.
Remarque : Les contraintes de la mesure de la chute nette
L'énergie nette est définie comme étant l'énergie hydraulique disponible à la turbine. Cette définition doit satisfaire des contraintes pratiques :
les limites géométriques contractuelles de la turbine,
la responsabilité à départager entre le turbinier et le civiliste,
le besoin de la mesurer avec précision.
La turbine est limitée par les sections de mesure haute et basse pression. Il y a donc une entente contractuelle qui définit leurs positions exactes.
Pour la section haute pression, c'est habituellement à l'entrée de la bâche spirale près de la jonction avec la conduite forcée. Il faut être suffisamment loin de toute discontinuité géométrique qui pourrait introduire des perturbations locales de l'écoulement.
Pour la section basse pression, c'est près de la sortie aspirateur mais suffisamment à l'amont pour éviter la perturbation crée par l'expansion brusque.
Fondamental : Élaboration de la définition de l'énergie nette
Pour la définition de la chute nette, on va reconstituer l'énergie locale à partir des mesures réalisables sur la machine. Considérons la figure ci-haut.
À l'entrée de la turbine :
On peut mesurer \(p_3\), \(z_3\) et l'énergie cinétique peut s'obtenir à partir du débit et être très représentative de l'énergie cinétique réelle :
\(E_{3}= \frac{p_3}{\rho} + g z_3 +\frac{\left(\frac{Q}{A_3}\right)^2}{2}\)
et on considère que \(E_{t3}=E_{3}\).
À la sortie de la turbine :
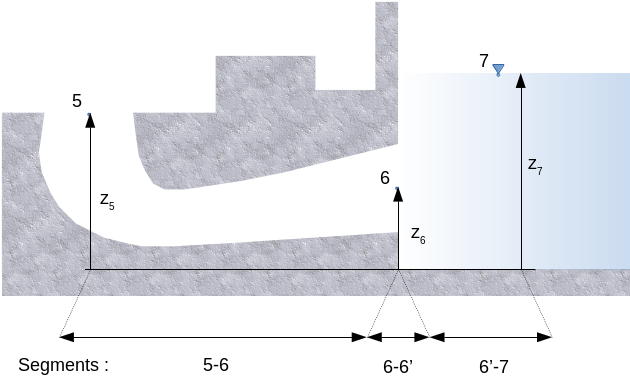
On peut mesurer la pression atmosphérique et le niveau aval \(z_7\) pour obtenir \(E_{t7}\).
De plus, on peut poser que \(E_{7}=E_{6'}\)
Sachant que \(E_{6'}=E_{6} - gh_{ns66'}\) où \(gh_{ns66'}\) est la perte de charge singulière entre le point 6 et 6' soit l'énergie cinétique à la sortie de l'aspirateur.
On peut alors écrire \(E_{6'}= \frac{p_6}{\rho} + g z_6\)
À cette étape, on considère que l'énergie à la sortie de la turbine s'obtient à partir des mesures au point 6.
L'énergie disponible devrait donc être la différence \(E_{3}-E_{6'}\).
Toutefois, pour le calcul de la chute nette, le CEI60193 considère que l'énergie cinétique à la sortie de l'aspirateur ne peut être inférieure à \(\frac{\left(\frac{Q}{A_6}\right)^2}{2}\). Elle donc doit être soustraite de l'énergie disponible.
Ainsi :
\(E=E_{3}-E_6'-\frac{\left(\frac{Q}{A_6}\right)^2}{2}\)
L'énergie nette devient donc :
\(E=\left(\frac{p_3}{\rho} + g z_3 +\frac{\left(\frac{Q}{A_3}\right)^2}{2}\right)-\left( \frac{p_6}{\rho} + g z_6+\frac{\left(\frac{Q}{A_6}\right)^2}{2}\right)\)
Il faut réaliser que \(\frac{p_6}{\rho} + g z_6+\frac{\left(\frac{Q}{A_6}\right)^2}{2}\) n'est pas l'énergie totale approximée en utilisant l'énergie cinétique basée sur la vitesse moyenne. Ce n'est pas une erreur ni un truc et ce n'est surtout pas l'énergie totale en 6.
Il en résulte que l'énergie nette ainsi définie représente bien toute l'énergie disponible que la turbine peut transformer en énergie mécanique et que c'est une base saine pour la définition du rendement.
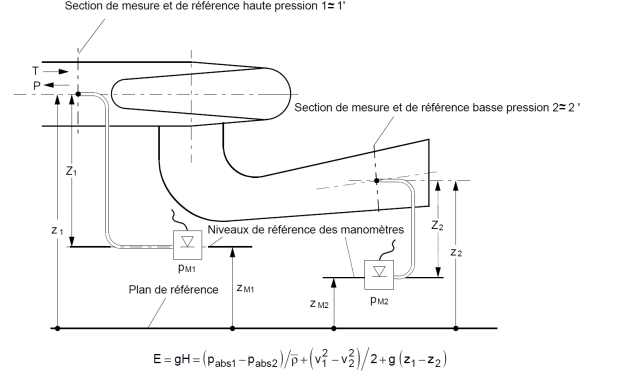
Définition : Définition de la chute nette suivant le CEI60193
Cette définition du CEI60193 s'appuie sur la connaissance des vitesses moyennes entrée et sortie (points 1 et 2 ici) qui sont calculées à partir de la mesure du débit et des sections haute et basse pression.
Un regard rapide à cette définition du CEI[4] pour la chute nette, nous porterait à penser qu'il s'agit de la différence de l'énergie totale entre l'entrée et la sortie de la turbine. Ce n'est pas le cas.
Les pressions statiques mesurées \(p_{abs1}\) et \(p_{abs2}\) en paroi sont très représentatives de la pression statique aux sections d'entrée et de sortie. Par contre, si \(\frac{(Q/A_1)^2}{2}\) basée sur la vitesse moyenne, représente assez bien l'énergie cinétique à l'entrée, ce n'est pas du tout le cas à la sortie. Ainsi à la sortie, l'énergie cinétique réelle est habituellement beaucoup plus importante que celle calculée par la vitesse débitante moyenne.
Cette caractéristique rencontre parfaitement nos exigences, ainsi le turbinier doit concevoir sa machine pour limiter au maximum l'énergie cinétique réelle à la sortie et ainsi maximiser l'énergie disponible à la roue. On observe aussi que l'énergie cinétique à la sortie basée sur la vitesse moyenne est le minimum possible à atteindre et le CEI considère qu'elle n'est pas disponible à la machine et donc est retirée de l'énergie nette. Cette portion de l'énergie cinétique ne pénalise pas le rendement.