Formulation avec les nombres de similitude et détermination d'un facteur de sécurité
La capsule Cavitation et Bernouli nous amène à une formulation plus élégante du point de fonctionnement critique en utilisant les nombres de similitude.
La définition du nombre de cavitation est à la capsule Le nombre de cavitation: définition et effet macroscopique sur le comportement de la turbine.
Fondamental : Formulation avec les nombres de similitude
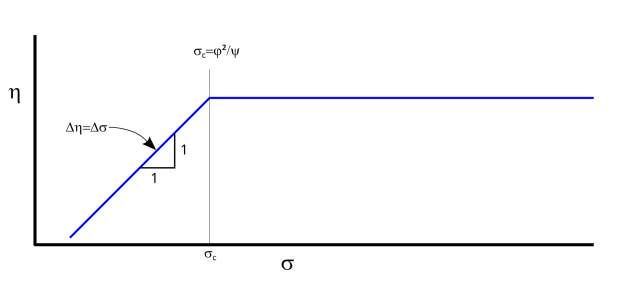
Pour un point de fonctionnement donné \((\varphi,\psi)\), la cavitation de sortie est établie quand on atteint le nombre de cavitation critique \(\sigma_c\) :
\(\sigma_c = \frac{\varphi^2}{\psi}\)
On peut trouver la définition des variables \(\varphi\) et \(\psi\ \)à la capsule Le système de l'EPFL \(\varphi \)- \(\psi\) et ainsi calculer le diamètre critique à partir du nombre de cavitation critique :
\(D_c=\left(\frac{8}{\pi^2}*\frac{Q^2}{E*\sigma_c}\right)^{\frac{1}{4}}\)
En réalité, on observe de la cavitation de sortie sous une plus haute pression. On peut toujours trouver une vitesse locale plus élevée que la vitesse moyenne. En plus, il y a des obstacle à contourner, les aubes et il y a des défauts géométriques locaux comme par exemple, les bords de fuites qui ont une épaisseur finie ce qui cause des accélérations locales.
On observe le phénomène à la capsule Observation de la cavitation dans le laboratoire hydraulique virtuel . Trois points de fonctionnement en rouge sur la colline y sont analysés pour la cavitation.
Pour mettre la roue à l'abri de la cavitation, il faut déterminer un sigma d'implantation plus élevé que le sigma critique qui lui demeure une référence analytique.
Fondamental : Détermination d'un facteur de sécurité sur la cavitation pour déterminer le diamètre
Il s'agit ici de déterminer le nombre de cavitation qui assure l'absence de cavitation.
Le but est d'éviter les effets néfastes de la cavitation entre autre les usures, le bruit, la perte de performance, etc.
Un critère qui semble faire consensus est l'apparition des bulles sur l'aubage. Ce critère est, en général, déterminé par l'essai sur modèle réduit. On trouve ainsi que le point de fonctionnement sécuritaire est situé à une valeur de sigma supérieur au sigma critique.
Comme mentionné dans la capsule citée plus haut, \(k_{\varphi\psi}\) détermine la qualité du tracé en localisant la valeur du sigma d'implantation (qui pourrait être noté ici : \(\sigma_p\)).
\(\sigma_p=k_{\varphi\psi}\frac{\varphi^2}{\psi}\) avec \(k_{\varphi\psi}\) toujours plus grand que 1.
Pour une turbine Francis moderne et bien conçue, il est en pratique autour de 1,8 lorsque la cavitation débute. Il se détermine au cours de l'essai modèle, en exécutant des dérives de sigma, ou par CFD[2]. Au début de la conception, ce chiffre devient un objectif de conception. Plus le chiffre est petit, plus les risques et les coûts de développement du tracé sont élevés mais plus la turbine est performante et économique. Si suite au développement, l'objectif n'est pas atteint, pour éviter les usures et les pertes de performances, il faudra augmenter le diamètre de la roue et/ou réduire la hauteur de sustentation, ce qui augmentera les coûts de réalisation.
Toutefois, si on dispose d'un profil hydraulique, les essais sur modèle réduit ou la CFD permettra d'évaluer ce facteur \(k_{\varphi\psi}\).
On peut donc calculer le diamètre pour une implantation à \(h_s\) et un \(k_{\varphi\psi}\) représentatif de la cavitation naissante ainsi :
\(D=\left(\frac{8}{\pi^2}*\frac{k_{\varphi\psi} Q^2}{E \sigma_c }\right)^{\frac{1}{4}}\)
Le résultat de \(\sigma_p = k_{\varphi\psi} \sigma_c\) est le sigma d'implantation. Il en résulte un \(h_s\) qui décidera des élévations pour le positionnement de la turbine dans la centrale.
À partir de l'observation lors des essais de cavitation sur modèle réduit, on peut déterminer pour le point de fonctionnement \((\varphi, \psi)\), le chiffre de cavitation « observation » correspondant à l'apparition des premières bulles et ainsi calculer le facteur \(k_{\varphi\psi}=\frac{\sigma_{obs}}{\sigma_c}\). On détermine ensuite le diamètre de la roue avec l'équation précédente.