Détermination du diamètre - Étude de cas
Exemple : Quel est le diamètre d'une turbine Francis de 150 MW sous 100 m de chute ?
Tel que formulé ce problème n'est pas complètement défini. D'autant qu'on n'a pas accès à un tracé hydraulique avec sa colline de rendement et ses dérives de sigma.
Si on revient à la formule : \(D=\left(\frac{8}{\pi^2}*\frac{k_{\varphi\psi} Q^2}{E \sigma_c }\right)^{\frac{1}{4}}=\left(\frac{8}{\pi^2}*\frac{k_{\varphi\psi} Q^2}{g \ NPSH}\right)^{\frac{1}{4}}\), voyons comment calculer cette valeur.
Q
Partant de la définition de la puissance et du rendement on établit que :
\(P = \rho Q \ g H \eta\) et donc que :
\(Q = \frac{P}{\rho \ g H \eta}\)
Posons les constantes \(\rho =1000\) kg/m³, \(g = 9,81\) m²/s.
Il reste \(\eta\) à définir, il s'agit du rendement à la puissance demandée de 150 MW. Ici, il nous faut faire une hypothèse sur la qualité de la conception et de la réalisation. Posons pour le rendement \(\eta = 93\)%, ce qui est tout à fait réalisable pour une turbine de cette puissance.
Donc toutes les varibles nécessaire au calcul du débit sont connues :
Q= \(\frac{150E06}{1000*100*9,81*0,93} = 164,4\) m³/s
Le NPSH
Il s'agit de l'autre variable nécessaire au calcul du diamètre.
\(NPSH = \left({h_{atm}+h_{faspi}-h_s-h_v} \right)\)
\(h_{atm}\) est la pression atmosphérique au bief aval.
\(h_v\) est la tension de vapeur à la température de l'eau.
Ici on pose les constante \(h_{atm}= 10\) mce et \(h_v = 0,2\) mce.
Pour une Francis, selon la qualité du tracé on attribue une valeur à \(k_{\varphi\psi}\), pour cet exercice proposons 1,8.
Pour la perte aspirateur, elle dépend de son rendement et de la section de sortie. Supposons une vitesse d'écoulement moyen de 2,25 m/s à la sortie de l'aspirateur au sommet de rendement. Si l'écart de rendement entre le sommet de rendement et la puissance maximale est de 1 %, on peut sans trop se tromper attribuer cet écart à la perte d'énergie cinétique. Ainsi, on assumera une perte aspirateur égale à la perte aspirateur au sommet de rendement plus la perte singulière additionnelle à la puissance maximale \(h_{faspi} = \frac{(2,25)^2}{2g}+ 0,01* 100 = 1,26\) mce.
Si nous enfonçons la roue 2 m sous le niveau aval, \(h_s=-2\) mce, on obtient :
\(NPSH=(10+1,26 -(-2)-0,2)=13,05\) mce.
Le \(k_{\varphi\psi}\)
Cette valeur est liée à la qualité du tracé en cavitation, il varie grosso modo entre 1,5 et 2,1 pour aller de la meilleure qualité à la moins bonne. Prenons pour cet exercice \(k_{\varphi\psi}=1,8\).
Maintenant on peut calculer le diamètre de la roue :
D= \(\left(\frac{8}{\pi^2}*\frac{1,8 *164,4^2}{9,81 *\ 13,05} \right)^{\frac{1}{4}}=4,189\) m
Avec toutes ces valeurs fixées, le diamètre (\(D\)) dépend directement de la hauteur de sustentation (\(h_s\)).
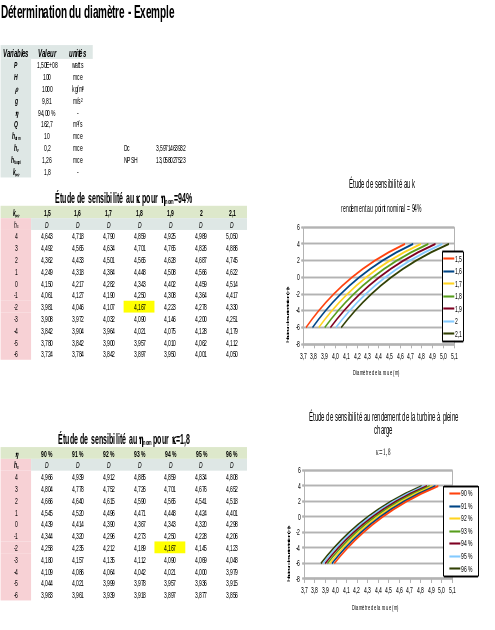
On pourrait tracer la relation \(D=f(h_s)\) mais pour les besoins de l'analyse on va étudier la sensibilité aux hypothèses faites sur le \(k_{\varphi\psi} \)et le \(\eta\) ainsi :
On s'aperçoit que la dimension de la turbine est influencée par la qualité du tracé en cavitation (\(k_{\varphi\psi}\)) et en rendement (\(\eta\)). Cette évaluation de la qualité se base sur l'expérience passée du concepteur et des ressources attribuées au développement du tracé et à la réalisation de la turbine. Néanmoins, il est ainsi possible de connaître le diamètre de la roue avec une précision suffisante. Il ne faut toutefois pas oublier que les coûts sont généralement proportionnels au poids qui lui varie au cube du diamètre.
À la lecture des tableaux, on voit que pour la plage des \(k_{\varphi\psi}\) envisagée à \(h_s = -2\) mce, la variation du diamètre est de ±4% alors que pour la plage des rendements supposée à la pleine charge, la variation du diamètre est de ±1,6%. En réalité, un hydraulicien expérimenté peut réduire significativement ces plages de prévision.