Formulation numérique inverse des deux plans conformes 2D vers la représentation dans le domaine 3D
Fondamental : Définition dans le plan méridien
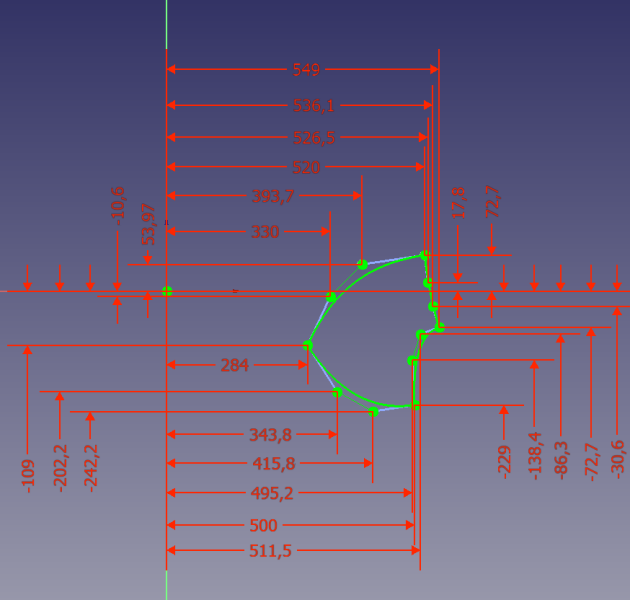
Il faut d'abord tracer les limites du tracé dans le plan méridien. On obtient les quatre courbes limites qui définissent le contour du tracé.
Donc, dans le plan méridien l'hydraulicien doit définir pour l'aubage, les quatre limites du carreau :
la face hydraulique du plafond ou moyeu et
la face hydraulique de la ceinture ou manteau, sur lesquelles l'écoulement glisse ;
le bord d'attaque et
le bord de fuite qui constituent une frontière que l'écoulement doit traverser pour effectuer son travail.
L'hydraulicien doit déterminer exactement la forme de ces limites. C'est là que des courbes de Bézier peuvent être avantageusement utilisées.
Ensuite, on utilise par interpolation dans le logiciel CAD[2] pour créer des courbes intermédiaires décrivant le transit du fluide entre les bord d'attaque et de fuite. On échantillonne chacune des courbes par une séries de point. Ces points de construction font partie de l'étape intermédiaire qui amènera la nouvelle géométrie en trois dimensions.
Pour chacune des courbes intermédiaires représentées par une série de points en \((r,z)\), on peut calculer :
les coordonnées (r,z) du bord d'attaque et du bord de fuite
la longueur curviligne \(m_j = \sum_{i=1}^{i=j}{\sqrt{(r_i-r_{i-1})^2+(z_i-z_{i-1})^2}}\)
Par exemple sur l'image suivante, la courbe considérée correspond à une coordonnée normalisé t=0,6. Son bord d'attaque et son bord de fuite correspondent respectivement aux coordonnées normalisées \((s=0,t=0,6)\) et \((s=1, t=0,6)\). Aussi l'échantillonnage correspond à des s spécifiques qui peuvent être avantageusement choisis équidistants. Ainsi s'il y a 9 points échantillonnés ils seront à \(s = 0 ; 0,125 ; 0,25 ; ... 1\) , c'est-à-dire par pas constant \(\Delta s = 0,0125\).
Définition : Correspondance entre la variable normalisée s et la position i dans les tableaux des autres coordonnées
Soit \(npt\) le nombre de points échantillonnés régulièrement le long d'un filet dans le plan méridien.
Le nombre de segment pour ce filet s'exprime donc \(nseg=npt-1\)
Le numéro de chaque point est identifié par i variant de \(0\) à \(npt\).
La coordonnée normalisée s se calcule :
\(s(i)={i\over nseg}\)
et le pas entre les point s'exprime :
\(\Delta s ={1\over nseg}\)
Pareillement, \({\Delta m = {m_{npt}\over nseg}}\).
Fondamental : Définition dans le plan de la cascade
À chacun des points i, pour i variant entre \(0\) et \(nseg\), dans le plan méridien correspond un point i dans le plan de cascade
À partir de l'expression analytique de \(u = \int_0^s{{dm\over ds}\over r} ds = \int_0^m{1\over r} dm\) où \(u(0)=0\)
On exprime dans le plan de la cascade la valeur de \(u\) qui varie de \(u(0)=0\) à :
\(u(nseg)= m(nseg) \sum_{i=1}^{i=nseg} {1 \over r(i)}(s(i)-s(i-1))\)
L'hydraulicien doit maintenant définir l'étalement angulaire de l'aubage soit les limites : \(v(0)=\theta (0)\) et \(v(nseg) = \theta_(nseg)\)
Donc on a ainsi déterminé, pour le plan de la cascade, les limites du tracé de la courbe considérée.
Pour tracer entre ces limites, l'hydraulicien doit déterminer la loi d'évolution de la position angulaire \(\theta\) entre les limites qui ont été déterminées. C'est là qu'une courbe de Bézier peut être avantageusement utilisée.
La courbe de Bézier peut maintenant être échantillonnée pour toutes les valeurs \(m(i)\) du plan méridien.
On obtient ainsi une série de points en \((u,v)\).
Où :
\(u(i)= m(i) \sum_{j=1}^{j=i} {1 \over r(j)}(s(j)-s(j-1))\)
\(v(i)\) est l'interpolation sur la courbe de Bézier qui correspond à la position de \(u(i)\) qui est définie suivant \(m(i)\).
Avec tous ces paramètres on a toute l'information pour tracer l'âme de l'aubage.
Fondamental : Définition dans le plan des longueurs
Pour éventuellement habiller l'aubage des épaisseurs souhaitées, il nous faut calculer la coordonnée \(n\) pour compléter la représentation dans le plan des longueurs. Ce plan est dédié aux respects des longueurs à obtenir dans le domaine en trois dimensions.
On a d'abord \(n(0) = r(0) * v(0)\) et pour les suivants :
\(n(i)=n(i-1) + r(i) * (v(i)-v(i-1))\)
On se rappellera ici qu'on ne peut utiliser la formulation \(n(i) = r(i) *v(i)\) parce qu'elle ne permet pas d'obtenir la conformité des longueurs entre le plan de cascade et le domaine 3D. La dérivée de la coordonnées transversale \(r\theta\) étant \(r d\theta\) et non \(d(r\theta)\).
Rappel : Résumé des paramètres nécessaires au tracé de la turbines
Dans le plan méridien
L'hydraulicien a établi le contour de l'aubage qui forme un carreau déformé. Chacun des côtés du carreau est une courbe de Bézier dont on a déterminé les pôles.
Il a déterminé le nombre de filets.
Il a déterminé le nombre de points par filet.
Il a déterminé par calcul les limites \(u_0\), \(u_n\), \(v_0\), \(v_n\) du plan conforme \(u-v\).
Dans le plan de cascade (u,v) conforme en angle
Il a déterminé les pôles de la courbes de Bézier représentant l'évolution de la position angulaire pour chacun des filets.
Fondamental : Définition dans le plan des épaisseurs
Maintenant on est à l'étape finition. On doit habiller le voile représenté par l'âme du profil d'une épaisseur.
Pour cette étape, un plan virtuel des épaisseurs est créé pour définir la loi d'épaisseur ou plus exactement les lois de demie épaisseur. On se référera à la capsule Génération de profil 2D pour la théorie sur la construction du profil à partir des lois de demie épaisseur.
La loi de demie épaisseur est modélisé dans un plan virtuel 2D des épaisseurs. On utilisera à cette fin les outils du modeleur géométrique pour construire le profil 2d à partir d'une forme à pôle.
Entre le point 1 au bord d'attaque et le point 5 au bord de fuite, on obtient la corde c'est à dire la longueur du profil.
Le point 2 permet de définir la tangence au bord d'attaque et la distribution de l'épaisseur locale dans son voisinage.
Le point 3 détermine l'amplitude et la position de l'épaisseur maximale.
Le point 4 définit la tangence au bord de fuite et la cambrure de la face dans son voisinage.
Pour un profil hydraulique, l'intégrité mécanique exige qu'on ne finisse pas un bord de fuite à son épaisseur nulle. On impose donc une troncature du profil à une épaisseur satisfaisante.
On obtient donc une demie loi d'épaisseur avec en abscisse la position sur la corde retenue pour la conception qui correspondra à la longueur du profil.
Si on exprime le plan virtuel des épaisseurs dans les coordonnées \((x, y)\), \(y(x)\) correspondra à l'épaisseur à la coordonnée \(x\) de ce plan.
Dans le plan des longueurs on fait correspondre la variable \(m(nseg)\) à la corde retenue pour la conception. Ainsi, on détermine le rapport d'échelle entre le plan des épaisseurs et la longueur du profil dans le plan méridien.
On doit échantillonner la corde retenue du nombre de points par filet et obtenir la demie épaisseur correspondant au profil.
La demie épaisseur s'ajoute donc selon l'ordonnée \(n\) dans le plan des longueurs qui est linéaire dans ce plan. On exprimera la demie épaisseur comme étant \(dn(s)\) pour la transposer dans le plan des longueurs.
\(\Delta n(i)= {y(i)\over {Corde_{retenue}}}\) avec \(s(i)={x(i)\over {Corde_{retenue}}}\)
Les demies épaisseurs intrados (\(\Delta n_i(i)\)) et extrados (\(\Delta n_e(i)\)) devraient être identiques pour conserver la définition de l'âme. Toutefois, pour des raisons pratiques, en cours de conception, il peut être utile des les différencier, tout en se rappelant que le cas échéant, l'âme ne représente plus les angles de l'écoulement.
On obtient donc pour \(m(i)\) les valeurs :
\(n(i)=n(i-1) + r(i) * (v(i)-v(i-1))\) pour l'ordonnée de l'âme
\(n_i(i)=n(i) +\Delta n_i(i)\) pour l'intrados
\(n_e(i)= n(i) + \Delta n_e(i)\) pour l'extrados
Maintenant on peut compléter le profil dans le plan u-v en ajoutant à l'âme, l'intrados et l'extrados ainsi :
Donc on obtient pour \(u(i)\) les valeurs :
\(v(i)\) pour l'âme qui comme on l'a vu provient de l'interpolation sur la courbe de Bézier dans le plan u-v
\(v_i(i)= v(i)+{\Delta n_i(i) \over r(i)}\)
\(v_e(i)= v(i)+{\Delta n_e(i) \over r(i)}\)
Fondamental : Construction du profil final dans le domaine 3D
À cette étape nous disposons de toutes les coordonnées des filets dans les plan des épaisseurs, des longueurs et de la cascade pour l'intrados, l'extrados et l'âme.
La construction du profil en 3D se calcule ainsi pour chacune des faces considérées (intrados, extrados, âme) :
x(i)=r(i)*cos(v(i))
y(i)=r(i)*sin(v(i))
z(i)
En complétant pour tous le filets et en assemblant on obtient le tracé de la roue.