Optimisation des dimensions à l'amont de la roue
Les autres facteurs dont dépendent les dimensions à l'amont de la roue
Le paragraphe précédent a démontré que pour le débit et la chute souhaité au point de rendement optimal, on a toute liberté de choix sur les trois variables qui décrivent l'entrée de la roue soit :
la vitesse angulaire \(\omega\) qui joue un rôle dans la transformation de l'énergie,
le rayon à la sortie du distributeur \(R_d\) et
la hauteur du distributeur \(b_d\) .
Pour fixer ces valeurs on doit optimiser d'autres critères qui assurent la faisabilité et la qualité de l'écoulement pour la cavitation et l'efficacité, les coûts de réalisation et d'autres variables incluant les critères de résistance des matériaux, d'exploitation de la machine, d'impact environnemental, etc. Pour y arriver, il faut utiliser des outils complexes comme la CFD, les éléments finis, choisir les matériaux, optimiser les achats et les procédés de fabrications. Il y aura toujours de l'empirisme à un moment donné ou à un autre dans ce processus. Toutes ces possibilités ouvrent la voie à l'innovation.
Détermination du canal à l'entrée de la roue sur des critères de conception hydraulique
Puisque le résultat de cette étude sera fort probablement analysé par CFD, il peut être pertinent de déterminer les variables \(R_d\) et \(b_d\) à partir de critères hydrauliques.
La détermination de diamètre de sortie de la roue a été basée sur des critères de cavitation, eux mêmes résultant d'une analyse économique de l'enfoncement. La vitesse méridienne qui en résulte ne peut être très différente de la vitesse méridienne à l'entrée de la roue :
\(X_{Cm}=\frac{Cm_1}{Cm_2}\cong 1\)
Une valeur inférieure à 1 nous amènera à des dimensions supérieures pour le distributeur et donc des coûts supérieurs mais avec l'avantage d'avoir moins de pertes hydrauliques et donc un meilleur rendement pour la turbine.
L'autre critère de conception est la déviation géométrique due à l'aubage soit :
\(X_{\Delta\alpha}= \alpha_2-\alpha_1\cong 0\)
Pour une roue dont le sens de rotation est positif, cette valeur est généralement négative. Plus cette valeur s'approche de 0 , plus l'écoulement suit un trajet court et donc efficace pour diminuer les pertes par friction mais au prix d'une augmentation des coûts de réalisation due à l'augmentation du \(R_d\).
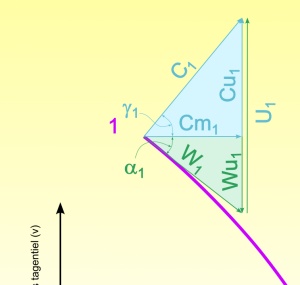
On peut à partir de ces valeurs définir les triangles des vitesses à l'entrée de la roue.
\(Cm_1=X_{Cm} Cm_2\)
\(\alpha_1= \alpha_2-X_{\Delta\alpha}\)
\(Wu_1=Cm_1\tan \alpha_1\)
\(U_1 =\frac{-W_{u1}+\sqrt{W_{u1}^2+4E_{Iopt}}}{2}\)
\(Cu_1=U_1-Wu_1\)
\(C_1=\sqrt{Cm_1^2+Cu_1^2}\)
\(\gamma_1=\arctan \frac{Cu_1}{Cm_1}\)
On peut maintenant en extraire les valeurs recherchées :
\(R_d=\frac{U_1}{\omega}\)
\(b_d=\frac{Q_{opt}}{2\pi R_d Cm_1}\)
Conclusion
Le but de cette discussion était de déterminer des critères de conception hydraulique qui permettraient d'obtenir la vitesse angulaire \(\omega\), le rayon à l'entrée roue \(R_d\) et la hauteur du distributeur \(b_d\).
On a vu que la vitesse angulaire dépend de la position du sommet de rendement et de l'angle à la sortie de la roue soit les variables \(X_Q\) et \(\alpha_2\).
Pour le rayon à l'entrée de la roue et la hauteur du distributeur, on ajoute \(X_{Cm}\) qui relie la vitesse débitante à l'entrée à celle à la sortie et \(X_{\Delta\alpha}\) qui détermine si la vitesse absolue dans la roue y est plus ou moins hélicoïdale.
Lors du calcul de la vitesse de rotation, on observe que la vitesse spécifique au point nominal est influencée par le fonctionnement au point optimal. On comprends qu'une même roue caractérisée par profil hydraulique conçue pour le point optimal peut être opérée au point nominal. Il s'agit néanmoins d'une caractéristique remarquable de la roue parce qu'elle est définie, du moins partiellement par la courbe de performance souhaitée. D'autre part, il faut souligner le paradoxe que la cavitation est indépendante de la vitesse de rotation mais que cette même cavitation nous permet de définir la vitesse de rotation.