Introduction
Comme on l'a vu, la sortie de la roue est la dimension principale de la turbine. Son rayon \(R\) est déterminé par le souci de maîtriser la cavitation de sortie. Il ne dépend ni de la vitesse de rotation ni de la chute.
La configuration des passages hydrauliques à l'amont doit considérer la transformation de l'énergie hydraulique en énergie mécanique. Ses dimensions fondamentales sont :
le rayon à la sortie du distributeur \(R_d\),
la hauteur du distributeur \(b_d\) .
L'approche monodimensionnel permet de représenter la roue par un seul filet fluide pour caractériser le comportement moyen de l'écoulement de l'amont (\(1\)) à l'aval (\(2\)) de la roue. Ce filet fluide est représenté en violet.
En appliquant la transformation conforme de Beltrami décrite ici, on « aplatit » la surface révolution sur lequel il est appuyé pour l'obtenir en deux dimensions soit dans le plan de la cascade (\(u-v\)). On peut ainsi représenter les triangles des vitesses en 1 et 2 et les calculer en fonction des dimensions fondamentale des la turbine.
L'objectif de conception
On pose l'objectif de conception au sommet de rendement. On y définit le débit \(Q_{opt} \)et la chute \(H_{Iopt}\).
Le triangle des vitesses à la sortie
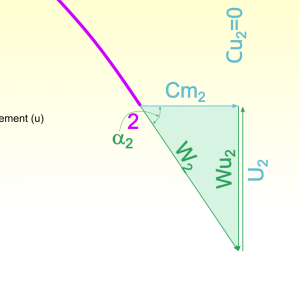
En posant l'objectif de conception au sommet de rendement, on vise une vitesse d'écoulement \(C_2\) parfaitement axiale à la sortie de la roue.
On a ainsi : la vitesse tangentielle du fluide à la sortie \(Cu_2=0\) et l'angle de l'écoulement dans le repère absolu \(\gamma_2=0\). La vitesse absolue \(C_2\) y est donc la vitesse débitante \(Cm_2\).
Ce faisant, on lie la vitesse de rotation à l'angle de l'écoulement dans le repère relatif \(\alpha_2\) et le triangle est entièrement connu avec :
\(Cm_2= \frac{Q_{opt}}{\pi R^2}\)
On choisit le \(r_2\) pour qu'il soit au milieu de l'aire de sortie de la roue. \(r_2=\frac{\sqrt 2}{2}\). On peut y calculer la vitesse tangentielle solide.
\(U_2=\omega r_2\)
Puisque l'écoulement est parfaitement axial :
\(Cu_2 = 0\)
\(\gamma_2=0\)
\(C_2=Cm_2\)
\(Wu_2 = -U_2\)
\(W_2 = \sqrt{Cm_2^2+Wu_2^2}\) et
\(\alpha_2=\arctan \frac{Wu_2}{Cm_2}\)
On s'aperçoit qu'à la sortie, seule la vitesse angulaire et le débit à l'optimum sont utilisés pour compléter le triangle des vitesses.
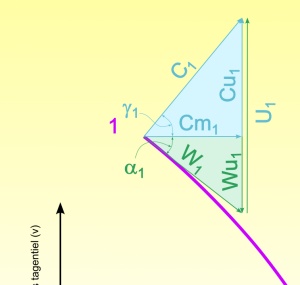
Les triangles des vitesses à l'entrée
À l'entrée de la roue, \(r_1=R_d\) et on peut y calculer la vitesse débitante à partir du débit Q_{opt} qui traverse la section annulaire du distributeur, on a donc aussi besoin de sa hauteur \(b_d\) :
\(Cm_1=\frac{Q_{opt}}{2\pi R_d b_d}\)
La vitesse de tangentielle solide (de la roue à cet endroit) y est : \(U_1 = \omega R_d\)
En utilisant La relation d'Euler au sommet de rendement toute l'énergie est concentrée dans la vitesse tangentielle fluide :
\(Cu_1=\frac{g H_{Iopt}}{ U_1}\)
Il en résulte la vitesse du fluide et son angle dans le repère absolu.
\(C_1=\sqrt{Cm_1^2+Cu_1^2}\)
\(\gamma_1=\arctan \frac{Cu_1}{Cm_1}\), ce qui complète le triangle des vitesses
absolues.
À partir de la vitesse tangentielle \(U_1\) on détermine le triangle des vitesses relatives :
\(Wu_1 = Cu_1 - U_1\)
\(W_1 = \sqrt{Cm_1^2+Wu_1^2}\) et
\(\alpha_1=\arctan \frac{Wu_1}{Cm_1}\)
De ces relations découlent la suivante qui est en redondance mais qui peut être utile :
\(U_1 =\frac{-W_{u1}+\sqrt{W_{u1}^2+4E_{Iopt}}}{2}\)
On constate donc que peu importe les 3 variables proposées, on obtiendra toujours des triangle de vitesse pour obtenir la performance désirée. Donc, la géométrie à l'entrée n'est pas définie par les seules conditions de fonctionnement. Il faut donc faire appel à d'autres critères d'optimisation.