Détermination de l'amont de la roue - Étude de cas
Exemple : Quelle est la géométrie amont de la roue Francis de 150 MW sous 100 m de chute ?
Un outil de dimensionnement est joint ici et reprend tous les calculs détaillés ci-bas.
Dans un paragraphe précédent Détermination du diamètre - Étude de cas on a déterminé, pour les mêmes conditions, le diamètre de la roue et son enfoncement. Ces variables servent donc de départ à notre exercice.
On sait que le sigma d'implantation est \(\sigma_p =0,1306\) et que le diamètre de sortie de la roue est \(D= 4,167\) m et donc \(R=2,083\) m. Ce calcul a été effectué pour la pleine charge sous la chute nominale où le rendement se situe à \(\eta_{nom}=94\)%.
Pour la géométrie à l'amont de la roue, on doit travailler avec le point de rendement maximum qui s'obtient avant d'atteindre la pleine charge. Supposons un sommet de rendement de 95% obtenu à 85% du débit de pleine charge.
\(X_Q=\frac{Q_{opt}}{ Q_{nom}}=0,85\)
\(Q_{opt}=X_Q*Q_{nom}=0,85*162,67=138,27\) m³/s.
Ce rapport s’applique aussi à la vitesse méridienne à la sortie \(Cm\).
Donc au point nominal on a \(Cm=\frac{Q_{nom}}{\pi R^2}=11,93\) m/s.
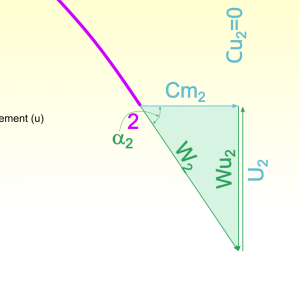
Au point optimal la vitesse méridienne sur la section donc aussi en 2 s’écrit :
\(Cm_2=Cm*X_Q=10,14\) m/s.
Vitesse angulaire
En souhaitant obtenir un angle \(\alpha_2=-70\) degrés on peut calculer la vitesse angulaire par :
\(U_2 =-Cm_2*tan(\alpha_2)=27,86\) m/s.
\(r_2=R*\frac{\sqrt 2 }{2}= 1,473\) m.
\(\omega = \frac{U_2}{ r_2}= \frac{27,86}{ 1,473}=18,91\) rad/s.
Il en découle que \(U=R \omega = 2,083*18,91= 39,39\) m/s.
Donc, on peut définir pour les points de fonctionnement les paramètres hydrauliques suivants :
Au point nominal :
\(\psi=\frac{2E}{\left(\omega R\right)^2}=\frac{2*981}{\left(18,91*2,083\right)^2}=1,264\)
\(\varphi_{nom}=\frac{Q_{nom}}{\pi \omega R^3}{U}=\frac{162,7}{\pi18,91*2,083^3}=0,303\)
Détermination du canal à l'entrée de la roue sur des critères de conception hydraulique
Posons \(X_{Cm}=\frac{Cm_1}{Cm_2}= 0,9\) et
\(X_{\Delta\alpha}= \alpha_2-\alpha_1=-10\) degrés. Ici, c'est le concepteur qui décide à partir de son expérience et ses calculs.
Pour les triangles des vitesses de sortie au point optimal :
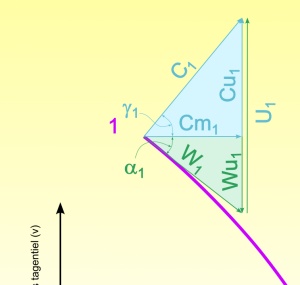
Pour les triangles des vitesses d'entrée :
\(Cm_1=X_{Cm} Cm_2= 0,9*10,14=9,13\) m/s.
\(\alpha_1= \alpha_2-X_{\Delta\alpha}=-70--10=-60\) degrés.
\(Wu_1=Cm_1\tan \alpha_1=9,13*\tan(-60)=-15,81\) m/s.
\(U_1 =\frac{-W_{u1}+\sqrt{W_{u1}^2+4E_{Iopt}}}{2}=\frac{--15,81+\sqrt{-15,81^2+4*932}}{2}=39,44\) m/s.
\(Cu_1=U_1+Wu_1=39,44-15,81=23,63\) m/s.
\(\gamma_1=\arctan \frac{Cu_1}{Cm_1}=\arctan \frac{23,63}{9,13}=68,88\) degrés.
Maintenant on peut extraire des vitesses d'entrée R_d et b_d :
\(R_d=\frac{U_1}{\omega}=\frac{39,44}{18,91}=2,085\) m
\(b_d=\frac{Q_{opt}}{2\pi R_d Cm_1}=\frac{138,27}{2\pi 2,085 * 9,127}= 1,156\) m.