Cavitation - Un phénomène à expliquer
Définition :
L'observation nous amène à définir la cavitation comme un phénomène diphasique résultant de la rupture du milieu continu de liquide sous l'effet de contraintes excessives [1]. On peut donc l'analyser à partir de mécanique des milieux continus puisque la rupture correspond à une limite de contrainte à ne pas dépasser. Cette limite est intimement liée à la température du fluide et est donc un phénomène thermodynamique.
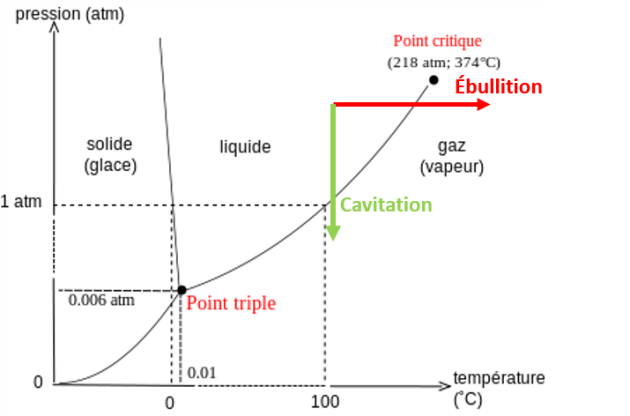
Effectivement, le diagramme de phase est un outil graphique intéressant pour étudier les transformations de phase. Il nous montre que le changement de phase est un phénomène singulier décrit par une frontière bien précise qui dépend de la température et de la pression du fluide. La cavitation y est donc définie comme étant un phénomène se produisant à température constante et à pression variable, ce qui est bien le type de milieu qu'on retrouve dans une turbine hydraulique. En effet, le franchissement de la frontière liquide-vapeur explique l'apparition et la disparition de la vapeur.
Le phénomène est donc lié directement à la pression absolue.
La nature instable de la cavitation en condition de laboratoire
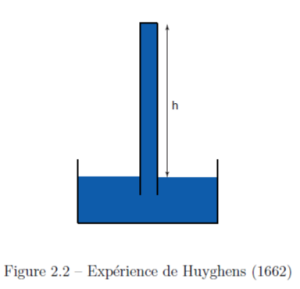
Dès 1662, Christian Huyghens a constaté une limite à la hauteur de la colonne de liquide dans une fiole inversée.
Par la suite, au dix-neuvième siècle, au cours d'essais répétés, variés et complexes dans plusieurs laboratoires, on a pu obtenir des valeurs de tension beaucoup plus élevées. La tension de rupture pouvant varier de -30 MPa à -500 kPa alors que les courbes de Van der Waals indiquent un minimum de -50 MPa.
Il en est ressorti que la tension de rupture est grandement influencée par les conditions d'essais, la nature des parois, la pureté de l'eau, ces variables étant plus ou moins maîtrisées lors des expériences d'où la grande variabilité des résultats. Il n'en demeure pas moins que ces valeurs élevées ne sont jamais atteintes dans les cas industriels.
Le comportement aléatoire observé est causé par des paramètres expérimentaux qui ne sont pas maîtrisés et qui ont échappés aux expérimentateurs.
Fondamental : La théorie des germes et la mécanique de la bulle unique
Il y a 3 étapes en séquence qui se produisent lors de la cavitation. Il y a l'initiation de la bulle de cavitation, sa croissance suivie de sa résorption. Il s'agit donc d'un phénomène dynamique. Blake en 1949 s'est intéressé à l'équilibre statique d'une bulle de cavitation. Il a ainsi pu expliquer le phénomène instable de la cavitation.
Reprenons son raisonnement. Soit l'existence dans le liquide d'une très petite bulle, nommée germe, sphérique de rayon \(r\) et remplie de gaz et vapeur.
Ici, l'idée fondamentale et innovatrice est de supposer que la très petite bulle de vapeur est polluée par une impureté soit un gaz.
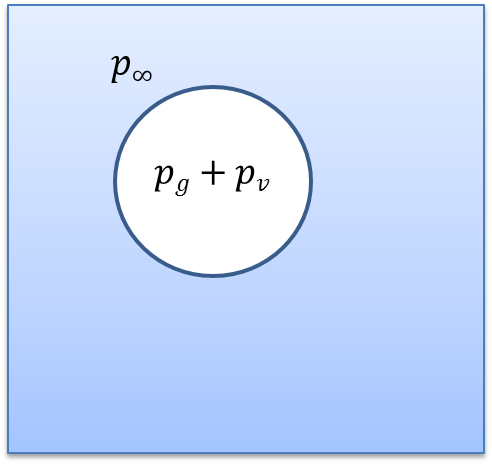
\(S\) est la tension à la surface de la bulle exprimée en N/m. On analyse l'équilibre de cette bulle dans son environnement en la coupant en 2 hémisphères pour y calculer les forces qui la maintiennent.
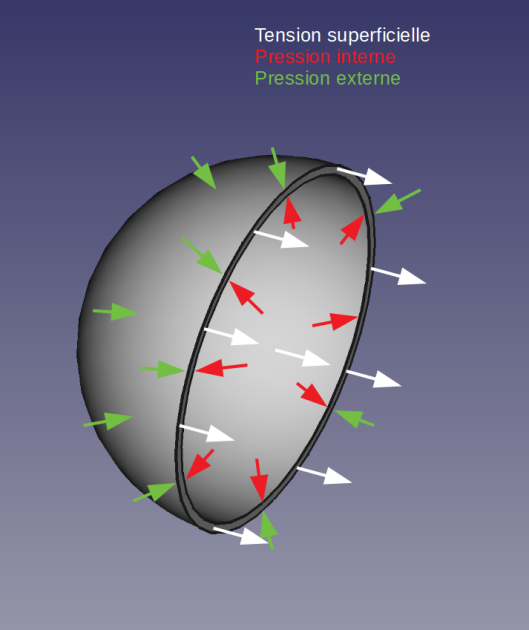
La force intérieure est due aux pressions partielles du gaz et de la vapeur agissant sur la section de la bulle et à la tension superficielle sur le périmètre de celle-ci :
\(F_{int}=(p_g+p_v)\ \pi r^2- 2 \pi r\ S\)
La force extérieure résulte de la pression ambiante agissant sur la section de la bulle :
\(F_{ext}=p_\infty \ \pi r^2\)
Par l'équilibre, les forces intérieure et extérieure sont égales :
\(p_\infty = p_g+p_v-\frac{2S}{r}\)
Pour une même quantité de gaz, sa pression dans la bulle est directement proportionnel au volume de la bulle.
Donc, si on se réfère à l'instant initial où la bulle a une quantité finie de gaz, on peut écrire :
\(p_\infty = p_{g0} {\left(\frac{r_0}{r}\right)}^3 +p_v -\frac{2S}{r}\)
Le traçage de cette fonction montre un minimum de pression (\(p_c\)) au rayon critique (\(R_c\)) :
\(R_c=\sqrt {\frac{3p_{g0}\ r_0^3}{2S}}\)
\(p_c=p_v-\frac{4S}{3R_c}\)
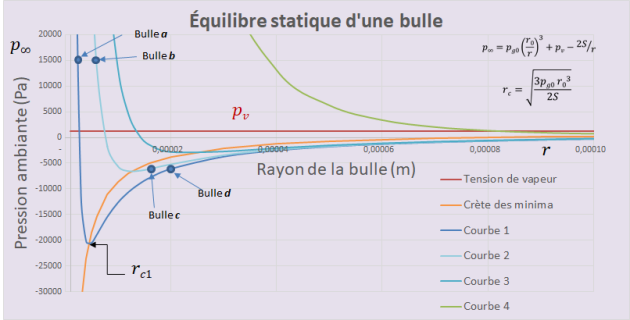
Sur le diagramme de l'équilibre statique d'une bulle, chaque courbe est obtenue pour une quantité de gaz constante qui croît de la courbe 1 à la courbe 4. Si, par un exercice de la pensée, on amène la bulle \(a\) au diamètre de la bulle \(b\) dans un environnement à pression constante, sa pression interne diminuera et la pression externe (identique pour les 2 bulles) ramènera la bulle à sa dimension d'origine. Donc, de ce côté du minimum de pression la situation est stable. Par contre, en se plaçant à droite du minimum, si on amène la bulle \(c\) à la dimension de la bulle \(d\), sa quantité de gaz étant plus élevée que \(d\), elle présentera une pression interne supérieure et ne pourra être ramenée par la pression ambiante à sa dimension originale. Cette région est donc instable.
La portion descendante des courbes est stable alors que la portion ascendante est instable (explosive?).
Le rayon critique défini la limite de l'existence statique et stable d'une bulle.
Il y a 2 possibilités:
Dans un écoulement, si ce rayon critique n'est pas atteint, la bulle maintiendra son équilibre.
Si ce rayon est atteint, sans autres considérations, il se produit un grossissement explosif. Il faudra utiliser les équations de la dynamique de la bulle pour expliquer son évolution d'une façon plus réaliste.
Il faut se rappeler que les germes ne peuvent exister que s'il y a un gaz autre que la vapeur.
Les germes très petits peuvent soutenir d'importantes tensions. La variabilité de la dimension des germes explique la variabilité des mesures de la tension de rupture d'un liquide qui a été constatée par de nombreux expérimentateurs.
Fondamental : L'équilibre dynamique d'une bulle
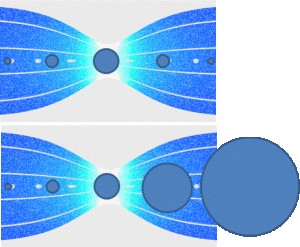
L'équilibre statique de la bulle a permis de mettre en exergue les paramètres qui expliquent les instabilités du comportement de la cavitation. On se doute bien que ces instabilités ne peuvent être illimitées et qu'il existe des freins à l'expansion du volume de la bulle. L'inertie du liquide environnant la bulle s'oppose évidemment à l'expansion de celle-ci et modifie le phénomène. La figure suivante illustre le phénomène, on retrouve en rouge la courbe telle que prévue par Blake et en vert une courbe plus réaliste résultant de l'équation de Rayleigh-Plesset[8].
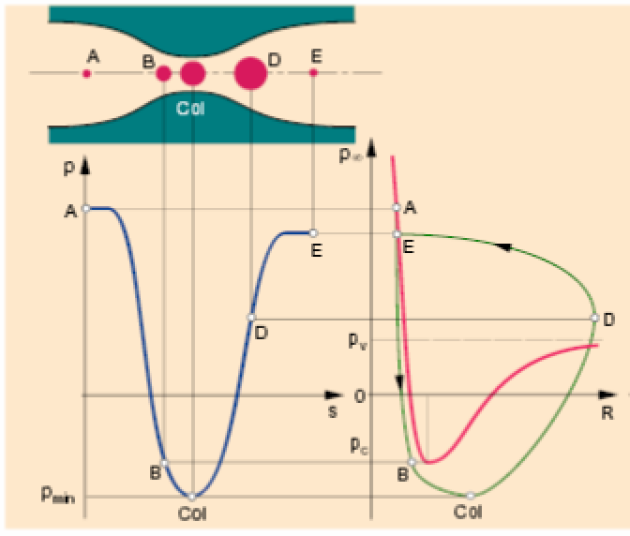
Cette équation se base sur les hypothèses de l'incompressibilité de l'eau et néglige les effets de viscosité et de la thermodynamique. Elle s'exprime ainsi :
\(p_\infty + \rho \left ( r \frac{d^2r}{dt^2} +\frac{3}{2} \left( \frac{dr}{dt}\right)^2\right)=p_g+p_v-2\frac{S}{r}\)
qui nous amène aux valeurs critiques suivantes :
\(R_c=\sqrt {\frac{3\left( p_\infty - p_v+\frac{2S}{r_0}\right)r_0^3}{2S}}\)
\(p_c=p_v-\frac{4S}{3R_c}\)
Ces raffinements permettent de se rapprocher de la réalité dans le suivi de la dimension de la bulle en fonction de la pression ambiante couvrant ainsi toute la séquence du phénomène : son initiation, sa croissance et sa résorption.