La relation d'Euler
Rappel : Leonhard Euler 1707-1783
Fondamental : Analyse d'une turbine élémentaire
C'est en généralisant l'énergie développée par un moulinet à tout type de condition d'entrée et de sortie qu'on obtient la relation d'Euler.
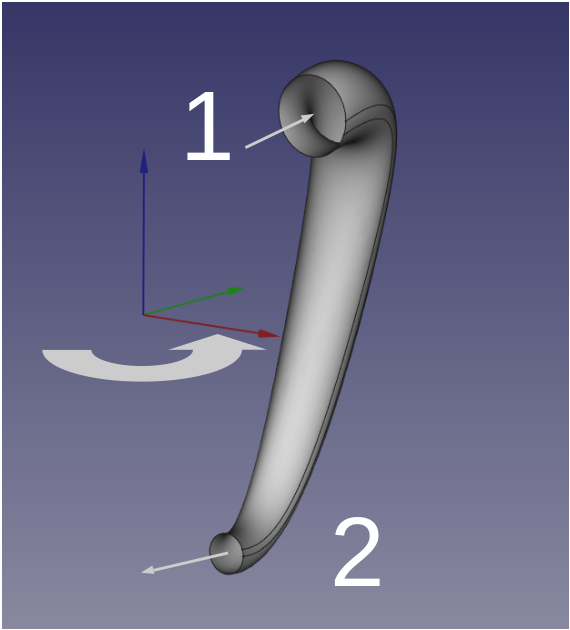
Pour la démonstration, considérons une turbine élémentaire constituée d'un tube à section variable dont l'entrée (indice 1) et la sortie (indice 2) sont tangentielles et parcourues par un débit de l'entrée vers la sortie. Le tube tourne autour d'un axe à une vitesse angulaire.
Considérons ce qui se passe à l'entrée en terme de quantité de mouvement.
L'effort tangentiel qui en résulte est positif et dans le sens de rotation : \(F_1 = \rho Q Cu_{1}\).
Le couple moteur est : \(M_1= r_1 \times F_1\) .
La puissance générée à l'entrée : \(P_1= \omega M_1\)
L'énergie à l'entrée s'exprime donc par : \(E_1 =U_1 Cu_{1}\)
Pour la sortie :
\(F_2=-\rho Q Cu_{2}\)
\(M_2 = r_2 \times F_2\)
\(P_2= \omega M_2\)
\(E_2 = -U_2 Cu_{2}\)
La puissance motrice résultant des vitesses à l'entrée et à la sortie sera : \(P=\rho Q (r_1\omega Cu_1 - r_2 \omega Cu_2)\)
Il en résulte la relation d'Euler permettant d'obtenir l'énergie générée par la turbine élémentaire :
Remarque :
La relation d'Euler nous indique que la puissance produite par une turbine vient de la déviation du filet fluide la traversant. Le même raisonnement s'applique à la pompe lorsque la puissance est négative, c'est-à-dire que la puissance doit être fournie pour générer le débit et la chute.
Dans cette présentation, pour simplifier, on a utilisé des entrée et sortie tangentielles. Dans une turbine réelle, l'écoulement n'est pas parfaitement tangentiel et pour appliquer la relation d'Euler il faut connaître les angles de l'écoulement pour en extraire les vitesses tangentielles \(Cu\) . Donc, connaissant les angles fluides à l'entrée et à la sortie d'une roue, on connaît l'énergie captée. L'efficacité énergétique et les pertes sont contenues dans les angles du fluide. C'est donc une affaire de géométrie.
On rappelle que la puissance est le produit d'un débit massique par une énergie massique.
On observe qu'il n'y aucune simplification ou hypothèse dans cette expression qui est exacte et que les notions de viscosité et turbulence ne sont pas utiles ici.
La relation d'Euler est l'équation maîtresse qui fait le lien entre l'énergie disponible et la géométrie de l'écoulement puis finalement la géométrie de la turbine.
Le concepteur hydraulicien doit donc générer une géométrie de roue avec les angles pour produire l'énergie souhaitée compte tenu de la vitesse de rotation.
Définition : L'énergie interne
L'énergie qui s'exprime ainsi aux bornes de la roue s'appelle l'énergie interne et peut se noter \(E_I\) ou \(gH_I\).
Complément : Généralisation du couple sur une cascade dans un repère cylindrique
Pour une cascade en rotation, puisque \(P = M \omega\), de la relation d'Euler :
\(P =\rho Q (r_1 \omega Cu_{1} - r_2 \omega Cu_{2})\), on peut écrire :
\(M=\rho Q (r_1 Cu_{1} - r_2 Cu_{2})\)
Également, pour une cascade fixe, à partir de l'équation de Newton adaptée au repère cylindrique : \(F=\rho Q(Cu_{1} - Cu_{2})\), on peut écrire :
\(M=\rho Q (r_1 Cu_{1} - r_2 Cu_{2})\)
On observe donc qu'on obtient la même équation pour le couple que la cascade tourne ou pas.
Complément : L'angle d'écoulement dans un tourbillon libre
Dans un repère cylindrique, \(r-z\), il y a un tourbillon libre, dont le moment cinétique s'y exprime au rayon \(R\) : \(\Gamma = R \ Cu\)
À la section de passage \(A\) correspondante à la position \(R\), la vitesse débitante \(Cm\) s'exprime par rapport au débit \(Q\) comme \(Cm = Q/A\).
L'angle de l'écoulement \(\gamma\) peut s'y exprimer ainsi : \(\tan \gamma=\frac{Cu}{Cm}\).
La géométrie du passage hydraulique permet de relier la position radiale \(R\) et la section de passage \(A\).
Par exemple dans un anneau fluide d'une hauteur \(B\),
\(A=2\pi\ R\ B\) exprime la section de passage de la vitesse débitante radiale.
Si on développe :
\(\tan \gamma=\frac{Cu}{Cm}=\frac{\Gamma/R}{\frac{Q}{2\pi\ R\ B}}=\frac{\Gamma}{Q}2\pi B\)
Le dernier terme de cette équation \(B\) étant une variable liée à la position, on peut conclure que l'angle de l'écoulement \(\gamma\) est connu.
Plus généralement, un tourbillon libre est caractérisé par un angle d'écoulement à la position considérée.
Fondamental : L'aubage en rotation dévie l'angle de l'écoulement
De part et d'autre de l'aubage, le long d'une ligne d'écoulement, il y a deux tourbillons libres caractérisés par leurs moments cinétiques qui, avec la vitesse débitante au point considéré, définissent les angles de l'écoulement.
C'est l'aubage et la vitesse de rotation qui dévient l'écoulement et en change les angles.
Méthode : Application au tracé d'une roue
Tracer l'aubage d'une turbine est le processus qui permet de relier les conditions hydrauliques et la performance souhaitée à la définition géométrique de l'aubage. Comme la relation d'Euler relie les conditions hydrauliques aux angles du fluide, il s'agit donc de créer une géométrie qui s'adapte à ces angles.
Les références Moulin[3] , Miller IV[4] , Rossgatterer[5] et plusieurs autres auteurs décrivent le développement que nous reprenons ici.
Ce développement s'appuie sur les concepts suivants :
La roue est constituée de plusieurs aubes, chacune possédant une surface intrados et une surface extrados. Un surface médiale virtuelle, ici appelée
« âme »
, peut en être déduite.
Le fluide dans la roue de la turbine se déplace en moyenne sur des surfaces de révolution qui intersectent le plan méridien pour former des courbes.
Le trajet de la particule fluide se déplaçant sur la surface de révolution, entre le bord d'attaque et le bord de fuite, trace une abscisse curviligne en trois dimensions qu'on peut nommer filet ou ligne de courant.
L'évolution des angles le long du trajet :
contribue, par la relation d'Euler à la transformation de l'énergie hydraulique en énergie mécanique.
et peut être représentée par une transformation conforme appelée transformation de Beltrami[7] qui est une sorte de mise à plat en deux dimensions de l'aubage (voir Plan de la cascade dans la figure suivante).
La projection cylindrique de ce trajet sur un plan méridien trace une abscisse curviligne en deux dimensions.
Brève explication de la transformation conforme de Beltrami
Avant d'arriver au plan conforme u-v, on passe par le plan des longueurs m-n où :
Avec \(m\) la longueur curviligne dans le plan méridien qui s'exprime en fonction de \(s\) :
\(m=m(s) =\displaystyle \int_0^s \sqrt {\left({dr \over ds}\right)^2+\left({dz \over ds}\right)^2} ds\)
Et \(n\) la longueur curviligne dans le sens transverse qui s'exprime aussi en fonction de \(s\) :
\(n=r\theta=r(s)\theta(s)\)
Ce plan des longueurs, n'est pas pratique pour suivre l'évolution des angles du filet et donc de l'écoulement. On a donc besoin de faire appel à un changement de coordonnées.
En divisant les coordonnées \((m,r\theta)\) par \(r\) on obtient les nouvelles variables suivantes :
\(u =\displaystyle \int_0^s{{dm\over ds}\over r} ds = \int_0^m{1\over r} dm\) où \(u(0)=0\) et
\(v(s)=\theta(s)\)
Ainsi, l'évolution de l'angle d'écoulement \(\alpha\) s'exprime :
\(\tan\alpha={rd\theta \over dm}={d\theta \over dm/r}={dv \over du}\)
Pour la méthode complète et le logiciel de génération d'un profil hydraulique cliquez ici.
Exemple : Recherche des angles moyens du fluide à l'entrée et à la sortie d'une roue Francis au point de rendement optimal
On utilise une approche unidimensionnel pour rechercher les angles moyens du fluide. En première étape pour une approche simplifiée, on pose les conditions suivantes :
L'aubage est représenté par une seule ligne de courant.
L'étude s'intéresse d'abord au fonctionnement au point de rendement maximum.
La rotation fluide \(Cu_{2}\) à la sortie de la roue est donc prévue nulle.
Sa géométrie 3D est complexe et se veut un assemblage de 2 plans orthogonaux correspondant respectivement au débit massique et à l'énergie massique
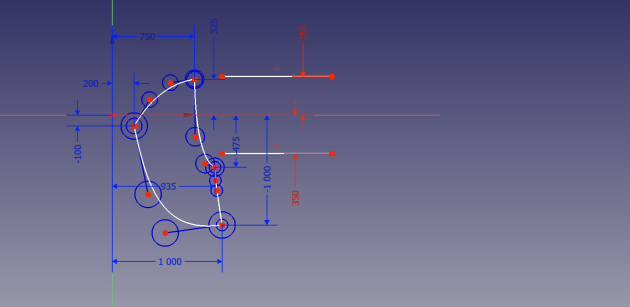
Plan méridien
Plan conforme de la cascade
La représentation de la roue dans les plans méridien et de cascade permet d'illustrer ces angles et les relations avec les vitesses d'écoulement lorsque la turbine fonctionne au point de meilleur rendement.
La géométrie de la roue est caractérisée par un rayon de sortie \(R\), un rayon d'entrée \(R_d\) et une hauteur du distributeur \(b_d\). La roue tourne à la vitesse angulaire \(\omega\).
Dans le plan méridien on a représenté l'écoulement moyen dans la roue par le filet fluide en violet et l'écoulement va du point 1 au point 2, passant d'une direction radiale à une direction axiale. Ce filet sépare la section de passage en deux sections de même grandeur. Ainsi le point 1 est est au rayon R_1=R_d et à la mi-hauteur du distributeur. Le point 2 est à la position \(R_2 = \frac{\sqrt 2}{2}R\) qui sépare la section de sortie en deux aires égales.
\(\frac{A}{2}=\frac{\pi R^2}{2}=\pi R_2^2\) et donc \(R_2=\sqrt{\frac{R^2}{2}}=\frac{\sqrt2}{2}R\)
Le plan de la cascade est orthogonal au plan méridien et permet de représenter les angles de l'écoulement.
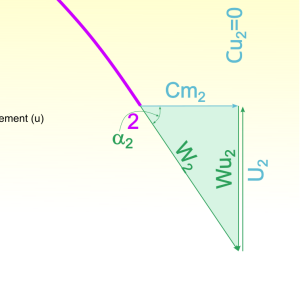
Au point 2, l'écoulement en 3D est axial. Dans le plan méridien l'écoulement y est représenté vertical et dans le plan de la cascade, il y est parfaitement horizontal.
Dans le plan de la cascade on représente l'angle de l'écoulement dans le repère tournant à la sortie de la roue \(\alpha_2\) qui s'exprime ainsi :
\(\alpha_2 = \arctan \left(\frac{-U_2}{Cm_2}\right)\) où les vitesses de rotation solide et débitante sont :
\(U_2 = R_2 \omega\)
\(Cm_2 = \frac{Q}{\pi R^2}\)
On note que la vitesse tangentielle de l'écoulement dans le repère absolu \(Cu_2\) est nulle parce qu'on est au point de meilleur rendement.
L'angle du fluide dans le repère absolue est donc : \(\gamma_2=0\)
La vitesse tangentielle relative s'exprime ainsi : \(Wu_2 = Cu_2-U_2 = -U_2\)
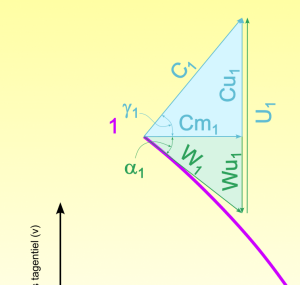
Au point 1, on est à l'entrée de la roue à la frontière avec le distributeur.
La vitesse de rotation solide y est : \(U_1 = R_d \omega\)
La vitesse débitante : \(Cm_1=\frac{Q}{2 \pi R_d b_d}\)
La vitesse de rotation absolue du fluide y est obtenue à partir de l'équation d'Euler : \(Cu_1= \frac{g H_I + U_2Cu_2}{U_1}\)
La vitesse de rotation relatif du fluide :\( Wu_1=Cu_1-U_1\)
L'angle de rotation relatif du fluide : \(\alpha_1 = \arctan \left({\frac{Wu_1}{Cm_1}}\right)\)
L'angle absolue du fluide y est : \(\gamma_1 = \arctan \left({\frac{Cu_1}{Cm_1}}\right)\)
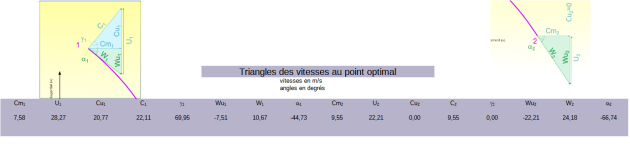
Exemple : Calcul des triangles des vitesses avec un exemple
Le fichier tableur décrivant cet exemple de calcul se trouve ici.
Soit une turbine qui se caractérise ainsi :
Densité du fluide \(\rho\)
Gravité \(g\)
Débit au point optimal \(Q_{opt}\)
Chute nominale \(H_{nom}\)
Rendement au point optimal \(\eta_{opt}\)
La chute interne au point optimal \(H_{I opt}\)
La vitesse de rotation \(n\)
La vitesse angulaire \(\omega\)
Les positions de ces cotes sont décrite sur le plan méridien de la roue.
En utilisant les équations précédemment décrites on calcule les triangles des vitesses.
Conseil : La forte sensibilité aux angles de l'écoulement
En manipulant le fichier joint, on peut observer la très grande sensibilité de la relation entre la performance et l'angle fluide à l'entrée \(\gamma_1\). Quelques dixièmes de degrés causent des variations en 1% du rendement. La CFD peut être utilisée avec précaution pour prédire ces angles et raffiner la conception de l'aubage avant la validation finale sur modèle réduit.