La similitude en vibration
Fondamental : Les conditions d'essais pour être en similitude de vibration
La vibration des turbines implique une interaction entre le fluide ou son écoulement et la structure.
Pour que deux systèmes en similitude géométrique soient en similitude de vibration, selon Tanaka[1], il faut que leurs ratios de fréquence naturelle mécanique (\(f_m\)) sur la fréquence d'excitation hydraulique (\(f_h\)), soient égaux sur modèle et sur prototype.
Donc pour un premier système noté (') et un second noté ('') , on peut écrire :
\(\frac{f_m'}{f_h'}=\frac{f_m"}{f_h"}\)
Avec la notation :
\(f_m^*=\frac{f_m'}{f_m"}\) et \(f_h^*=\frac{f_h'}{f_h"}\)
On obtient :
\(f_m^*=f_h^*\)
Le \(f_m^*\)représente le ratio des fréquences naturelles de deux systèmes élastiques. On suit le même principe de nomenclature que celui défini ici.
On peut donc écrire pour des systèmes élastiques en vibration sans amortissement les équations décrivant leur ratio de fréquence naturelle \(f_m^*\) :
\(f_m^*=\sqrt {\frac{K^*}{M^*}}\)
Sachant que pour une structure élastique on peut exprimer les forces en fonction des déplacements :
\(F=K x\)
et les contraintes en fonction des déformation :
\(\sigma=E_y\varepsilon\rightarrow \frac{F}{A}=E_y\frac{x}{L}\)
on obtient donc que le ratio des rigidités entre les deux systèmes est :
\(K^*=L^*E_y^*\)
et puisque :
\(M^*=\rho^*L^{*3}\)
on obtient pour le ratio des fréquences propres :
\(f_m^*=\frac{1}{L^*}\sqrt{\frac{E_y^*}{\rho^*}}\)
De son côté, le \(f_h^* \)représente le ratio des fréquences d'excitation de deux systèmes d'écoulement. Se basant sur le nombre de Strouhal exprimant que le ratio de la distance parcourue par l'écoulement par rapport à la structure pendant une période de temps est une échelle conservée entre deux systèmes d'écoulement en similitude, on peut écrire :
\(St=f_h\frac{L}{V}\)
\(f_h^*=\frac{V^*}{L^*}=\frac{\sqrt H^*}{L^*}\)
La condition \(\frac{f_m^*}{f_h^*}=1\) se construit en sachant que :
\(f_m^*=\frac{1}{L^*}\sqrt{\frac{E_y^*}{\rho^*}}\)
et
\(f_h^*=\frac{V^*}{L^*}=\frac{\sqrt H^*}{L^*}\)
\(\frac{f_m^*}{f_h^*}=\sqrt{\frac{E_y^*}{\rho^*H^*}}=1 \rightarrow H^*=\frac{E_y^*}{\rho^*}\)
Complément : Discussion sur les similitudes qui peuvent être conduites simultanément à celle en vibration
De ce résultat, on peut déduire que :
Les matériaux des structures en similitude, caractérisés par leur module de Young et leur densité, imposent la chute de l'essai pour obtenir la similitude en vibration.
Avec le même matériau sur modèle et sur prototype, on se doit donc de conserver la chute prototype pour conduire les essais sur modèle.
L'échelle des structures n'a pas d'effet sur la similitude en vibration. Cette liberté est d'un point de vue pratique soumise à la contrainte que la chute d'essai et la dimension du modèle sont limités par la puissance disponible à la plate-forme.
Si on souhaite une similitude du comportement de la torche qui est une structure dysphasique allongée verticalement, les similitudes de Froude et de cavitation doivent être respectées. Cela impose que \(L^*=H^*\), soit que l'échelle du modèle corresponde à l'échelle de la chute. Cette condition permise par la similitude en vibration soumet le modèle à une chute très faible et à des conditions de vide dans le circuit difficiles à mettre en œuvre.
Il faut quand même observer que la torche est une source d'excitation significative et que le respect de sa similitude sur modèle est souhaitable dans le cadre d'une étude des vibrations.
Pour avoir la similitude des déformations et des vibrations simultanément, comme pour le premier \(H^*=E_y^*\) et que pour le second \(H^*=\frac{E_y^*}{\rho^*}\), la la densité des matériaux de la structure doit être la même sur modèle et sur prototype.
Exemple : Pour choisir un matériau pertinent
En pratique, il est plus facile de conduire des essais sur modèle sous chute réduite. Il convient donc de rechercher un matériau dont le \(\frac{E_y}{\rho} \)soit le plus petit possible.
Voici donc une liste de matériaux dont on peut s'inspirer pour rechercher le matériau adéquat en fonction des similitudes recherchées. On y a exprimer, le ratio des chutes obtenues en assumant que le prototype est en acier. Évidemment, les chiffres donnés sont approximatifs et des certificats des matériaux doivent être obtenus pour plus de précision.
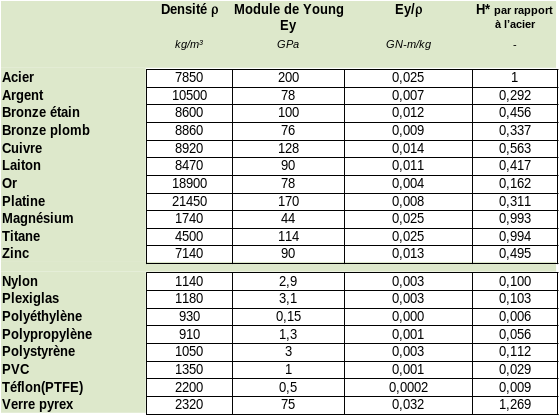
On observe que le bronze de plomb présente des propriétés qui permettent de faire l'essai sur modèle à un tiers de la chute du prototype et compte tenu de son prix, il est certainement intéressant. L'argent a déjà été utilisé par le laboratoire d'Andritz à Gratz qui depuis, conserve leur roue modèle sous clé ...
Aussi, les polymères peuvent s'avérer intéressants en permettant de réduire la chute du modèle sous le dixième de la chute du prototype. Comme la technologie du prototypage rapide par addition est de plus en plus accessible, c'est certainement une piste à explorer. De plus, comme les polymères sont des résines, ils peuvent être chargé de matière massive pour accentuer leur propriété. Leur potentiel est donc intéressant.