Étude de l'aspirateur
Fondamental : Calcul de la perte aspirateur
Les fonctions de l'aspirateur sont :
Retourner l'eau à la rivière
Diminuer l'énergie cinétique à la sortie
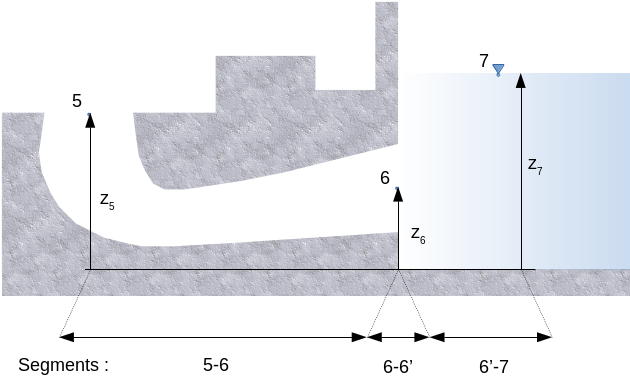
Considérons un aspirateur fonctionnant au sommet de rendement. L'entrée est en 5 et la sortie en 6. Le point 7 est situé à la surface du niveau aval.
Le point 5, situé sous la roue, présente une énergie totale qui s'exprime par l'équation de Bernoulli :
\(E_{t_5} = {p_5 \over \rho} + g z_5 + {{v_5}^2 \over 2 }\)
En 7, la pression statique est la pression atmosphérique, l'énergie potentiel est \(\rho\), \(g\), \(z_7\) et l'énergie cinétique est nulle :
\(E_{t_7} = {p_{atm} \over \rho} + g z_7\)
Le point 6 se situe sur une discontinuité entre le segment 5-6 et le segment 6-7, appelons-le segment 6-6'. En fait, dans le segment 6-6', l'écoulement subit une expansion brusque de la section 6 vers une section infini en 7. Il ne s'agit plus d'un écoulement divergent et l'énergie cinétique en 6 est totalement perdue.
C'est une perte singulière qu'on note \(g h_{ns_6}\) selon la nomenclature du code CEI60193 où l'indice \({ns}\) signifie non-scalable c'est à dire singulière et plus loin on utilisera l'indice \(s\) qui signifie scalable pour les pertes par friction.
\(g h_{ns_6} = E_{t_{6}}-E_{t_{6'}} = {{v_6}^2 \over 2}\)
On peut écrire sur les énergies totales en 6' et en 7 :
\(E_{t_{6'}} = E_{t_7}\)
Considérant \(g h_{s56}\) les pertes par frictions entre 5 et 6, si on exprime les niveaux d'énergie totale en 5, 6 et 7, :
\(E_{t_5} = E_{t_6} + g h_{s56}\)
\(E_{t_6} = E_{t{6'}}+gh_{ns_6}\)
\(E_{t_6}= E_{t_7}+gh_{ns_6}\)
Donc :
\(E_{t_5} = E_{t_7}+g h_{ns_6} + g h_{s56}\)
La perte aspirateur est donc :
\(E_{t_5} - E_{t_7} = g h_{ns_6} + g h_{s56}\)
On observe que l'énergie cinétique en 6 augmente l'énergie totale en 5 peu importe l'énergie en 7. Il s'agit donc d'une perte qui diminuera l'énergie disponible à la roue et qui ne sera, bien évidemment, pas transmise à l'arbre.
Il y aura donc avantage à diminuer l'énergie cinétique à la sortie de l'aspirateur en maximisant la section à cet endroit.
Exemple : Approche de la réalité : un exemple d'un calcul CFD dans l'aspirateur
Bernoulli est l'équation de l'énergie et dans le développement précédent nous avons considéré la perte charge (\(g h_{s56}\)) (pertes par friction paroi et fluide). Le calcul CFD[1] nous permet de la calculer. Une des caractéristique du calcul CFD est qu'il se fait sans effet de gravité, on observe aucune interaction entre l'énergie potentielle et le comportement de l'aspirateur.
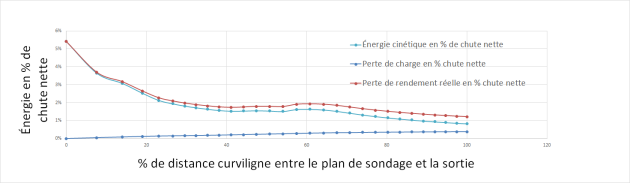
Sur le graphique, on considère un aspirateur dont la longueur varie le long de l'abscisse curviligne. Donc pour chaque point le long de l'abscisse on calcul les pressions et énergie cinétique à chaque point comme s'il s'agissait de la sortie de l'aspirateur.
Donc, s'il n'y avait pas d'aspirateur pour le calcul montré, l'énergie à la sortie de la turbine serait de 5,41% et cette énergie serait perdue.
Au fur et à mesure qu'on allonge l'aspirateur, l'énergie cinétique (\(g h_{ns6}\)) décroît alors que la perte par friction (\(g h_{s56}\)) croît. Il en résulte globalement une réduction de l'énergie. De sorte, qu'à la sortie, l'énergie est réduite à 1,21%.
On peut aussi extrapoler qu'en allongeant l'aspirateur, on obtiendra une plus grande énergie à la roue.
Il est remarquable d'observer que l'aspirateur montré, au point de rendement sommet, contribue pour 4,2% d'augmentation de rendement.
Plus généralement, une turbine fonctionne au point optimal avec une vitesse axiale à la sortie de la roue d'environ 10 m/s ce qui correspond a une énergie cinétique d'environ 5 mce[2] et ceci peut importe la chute à exploiter. Donc, sous les basses chutes la contribution de l'aspirateur peut être très importante, par exemple 20% de rendement pour une chute de 25 m.
