L'équation de Bernoulli - conservation de l'énergie [Turbines hydrauliques

L'équation de Bernoulli - conservation de l'énergie

Fondamental : Daniel Bernoulli 1738

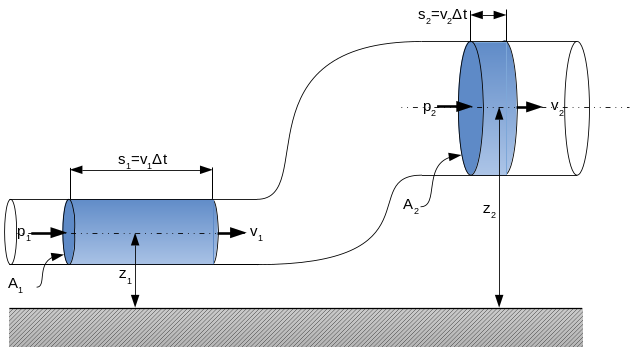
Conservation de l'énergie avec Bernoulli | Informations^[1]

Pour étudier l'écoulement d'un fluide incompressible et idéal dans un conduit quelconque, considérons un débit permanent (\(Q\)) qui nous donne un volume et donc une masse (\(m\)) s'y déplaçant pendant le temps Δt :

Dans la zone 1 à section constante \(A_1\), pour le débit \(Q\) on obtient la vitesse \(v_1=Q/A_1\) et le fluide parcourt la distance \(s_1\). La position en altitude y est exprimée par \(z_1\) par rapport à une référence. L'axe \(z\) pour l'énergie potentielle est positive vers le haut.
Dans la zone 2 par conservation du débit \(Q\) on obtient la vitesse \(v_2=Q/A_2\) et le fluide parcourt la distance \(s_2\). La position en altitude y est exprimée par \(z_2\).

Pour les zones 1 et 2, la conservation de l'énergie nous indique que les sommes du travail massique (\(W\)) et des énergies massiques cinétique (\(E_c\)) et potentielle (\(E_p\)) sont égales et donc constantes.

Ce qui s'exprime par :

\begin{matrix} W_{1} + E_{p 1} + E_{c 1} = W_{2} + E_{p 2} + E_{c 2} \\ où \\ E_{pi} = g z_{i} \\ m E_{ci} = m \frac{v_{i}^{2}}{2} \to E_{ci} = \frac{v_{i}^{2}}{2} \\ m W_{i} = p_{i} A_{i} s_{i} = p_{i} A_{i} v_{i} Δ t \\ ρ Q Δ t W_{i} = p_{i} Q Δ t \\ W_{i} = \frac{p_{i}}{ρ} \\ En assemblant : \\ \frac{p_{1}}{ρ} + g z_{1} + \frac{v_{1}^{2}}{2} = \frac{p_{2}}{ρ} + g z_{2} + \frac{v_{2}^{2}}{2} \\ \frac{p_{i}}{ρ} + g z_{i} + \frac{v_{i}^{2}}{2} = Constante \end{matrix}

En mécanique des fluides, le principe de Bernoulli statue que dans le flux d'un fluide où l'énergie se conserve, une accélération se produit simultanément avec la diminution de la pression.

Définition : Quelques définitions découlant de l'équation de Bernoulli

On appelle énergie totale \(E_t\) , l'énergie calculée par Bernoulli à une section i d'un conduit.

\(E_{t_i} = {p_i \over \rho} + g z_i + {{v_i}^2 \over 2 }\)

On appelle perte de charge \(g h_f\) ,la différence d'énergie totale entre deux sections d'un conduit.

\(g h_{f12} = E_{t_1} - E_{t_2}\)