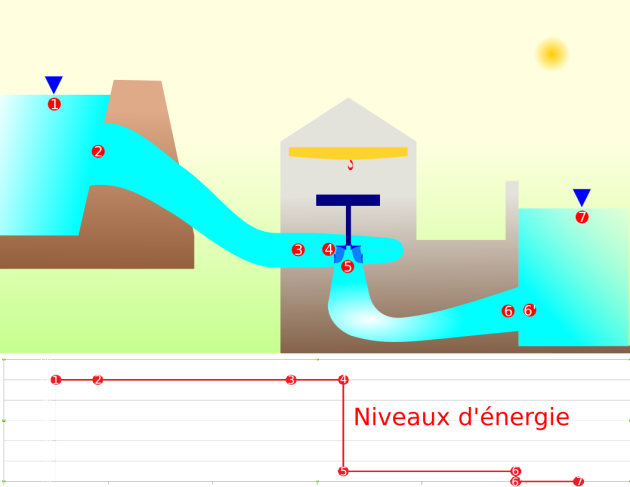
Le cheminement de l'énergie hydraulique dans une installation hydroélectrique
L'énergie disponible pour une centrale hydroélectrique se perçoit assez facilement en visualisant la différence des niveaux entre le bief amont et le bief aval. Il s'agit de l'énergie brute disponible sur le site. Bien entendu, lors de l'écoulement, à cause de la friction, des pertes de charges sont générées mais elles sont en général assez faibles.
En suivant l'écoulement de l'amont vers l'aval, on parcours les points suivants :
Au bief amont, on retrouve une surface libre à une altitude z qui est la plus importante du circuit. La vitesse de l'écoulement y est nulle et la pression ambiante est la pression atmosphérique. De ces valeurs on peut y calculer une énergie totale avec l'équation de Bernoulli.
À la prise d'eau, l'énergie totale est très voisine de celle du point 1 mais on y retrouve une altitude inférieure, une vitesse d'écoulement faible mais calculable en connaissant le débit et la section d'entrée et la pressions ambiante peut être calculée en utilisant l'équation de Bernoulli.
Alors que les points précédents sont réputés ne pas faire partie de la turbine, le point 3 est à la frontière amont qui détermine le début de la turbine, on y retrouve les prises de pression. La pression statique qui y est mesurée, la pression dynamique qui peut être déterminée à partir du débit et de la section aux prise de pression ainsi que l'altitude moyenne de cette section permettent de calculer l'énergie totale en utilisant l'équation de Bernoulli. Encore une fois, cette énergie est très voisine de celle du point 1.
L'eau entre maintenant dans la roue. Son énergie est voisine de celle du point 1 mais elle est très exactement égale au produit de la vitesse tangentielle du solide et de la vitesse tangentielle du fluide selon la relation d'Euler. Toutes les pertes de charge entre le point 1 et le point 4 sont incorporées dans la vitesse tangentielle du fluide. On peut aussi calculer l'énergie totale à ce point en y appliquant l'équation de Bernoulli et on trouvera la même valeur.
L'eau sort de la roue. L'énergie y est sensiblement inférieure à celle à l'entrée parce qu'absorbée par l'arbre. Comme pour le point 4, l'énergie y est très exactement égale au produit de la vitesse tangentielle du solide et de la vitesse tangentielle du fluide selon la relation d'Euler. Cette valeur peut aussi y être calculée par l'équation de Bernoulli. On observera qu'elle n'est pas du tout voisine de celle des points 4 et précédents. La roue crée une discontinuité dans la courbe de distribution de l'énergie.
L'eau s'engage maintenant dans l'aspirateur pour retourner à la rivière mais aussi pour en diminuer l'énergie cinétique.
Nous voici à la frontière aval qui détermine la fin de la turbine. Les prises de pression en sont la frontière physique. Ce point se trouve aussi à cheval sur une discontinuité géométrique.
Il fait partie de l'aspirateur et en ce sens son énergie calculée par Bernoulli est très voisine de celle du point 5.
Il fait aussi partie de la rivière et en ce sens son énergie calculée par Bernoulli est très voisine de celle du point 7.
En fait, l'énergie cinétique résiduelle à la sortie de l'aspirateur est perdue et crée une discontinuité dans la courbe de distribution de l'énergie. Cette perte est calculée en considérant l'équation de perte dans une expansion brusque.
Au bief aval, on retrouve comme au point 1, une surface libre. La vitesse de l'écoulement y est nulle et la pression ambiante est la pression atmosphérique. Cela nous permet d'y calculer l'énergie totale avec l'équation de Bernoulli et cette énergie est la plus basse du circuit.
Sur cette figure, on illustre la position des points et les niveaux d'énergie associés. On constate que la roue provoque une discontinuité dans la distribution en absorbant l'énergie selon la relation d'Euler et qu'à la sortie de l'aspirateur, l'énergie cinétique résiduelle y est perdue ce qui crée aussi une discontinuité.