Le traitement des pertes par le CEI60193
Le bilan des pertes
Selon le CEI, les pertes sont divisées en :
pertes hydrauliques
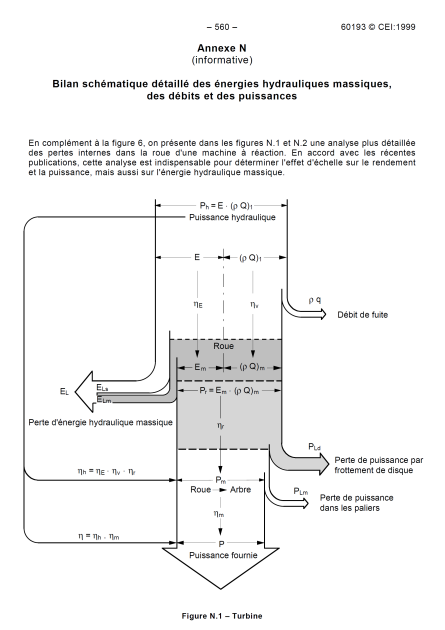
\(E_L\) est la perte d'énergie hydraulique massique entre la section haute (basse) pression et la section basse (haute) pression d'une turbine (pompe). Soit la somme de :
\(E_{Lm}\) est la perte d'énergie hydraulique massique dans les canaux de la roue.
\(E_{Ls}\) est la perte d'énergie hydraulique massique dans les pièces fixes.
pertes de débit
\(\rho q\) est le débit massique qui contourne la roue. Sur une Francis, c'est par les labyrinthes au plafond et à la ceinture. Sur une Kaplan c'est entre la pale et le manteau de roue et entre la pale et le moyeu.
pertes de puissance.
\(P_{Ld}\) est la puissance hydraulique dissipée entre la surface disque extérieure de la roue et les parois fixes.
\(P_{Lm}\) est la puissance hydraulique dissipée dans les paliers.
L'effet d'échelle calculé par le CEI ne s'occupe que des pertes hydrauliques, les pertes de débit et de puissance devront être traitées à part.
On sait qu'il y a 2 types de perte hydraulique :
les pertes par frictions et
les pertes singulières.
Le coefficient des pertes par frictions varie avec le nombre de Reynolds comme on l'a vu avec le diagramme de Moody. C'est donc une variation prévisible et c'est celle qui cause l'effet d'échelle. Comme le passage du modèle au prototype s'accompagne d'un accroissement du nombre de Reynolds par l'augmentation de la dimension et de la chute donc de la vitesse. À un nombre de Reynolds supérieur on aura donc un coefficient de perte inférieur et donc un rendement supérieur.
Fondamental :
Essentiellement, le code CEI impose les hypothèses suivantes :
les surfaces mouillées sont hydrauliquement lisses,
le point de calcul est le sommet de rendement,
on y trouve les pertes singulières (\(\delta_{ns}\)) les plus faibles et elles sont indépendantes de l'échelle
Les pertes transposables (\(\delta\)) y sont variables avec le Reynolds
Toutefois, pour un Reynolds constant, les pertes transposables (\(\delta\)) sont les mêmes peu importe le point de fonctionnement
Il en résulte que la variation de rendement entre le modèle et le prototype est constante pour tous les points de fonctionnement
Pour un point de fonctionnement à \(Re\) variable (même point sur 2 turbines similaires) | Pour différents points de fonctionnement à \(Re\) constant (sur une même colline pour la même turbine) | |
Pertes singulières (\(\delta_{ns}\)) | sont constantes | varient |
Pertes de friction (transposables) (\(\delta\)) | varient | sont constantes |
Pour le point de meilleur rendement :
Les pertes singulières (\(\delta_{ns}\)) sont constantes peu importe le Reynolds
Les pertes transposables (\(\delta\)) sont variables avec le Reynolds
La proportion entre ces deux types de pertes ( \(V_{ref}= \delta/(1-\eta_h) \)) est fixée à un Reynolds \(Re_{ref}\) de 7*106 et présente une valeur standard qui dépend du type de machine.
Rappel : Les pertes sont exprimées en pourcentage de la chute.
Définition : Mécanisme en place pour le calcul de l'effet d'échelle
Le \(V_{ref}\) est donc une valeur statistique.
Voici les valeurs de \(V_{ref}\) pour les différents types de turbine.
Les turbines à double réglage montrent des pertes singulières plus faibles parce qu'il y a moins de chocs.
Les valeurs de \(V_{ref}\) indiquées au tableau 7 sont rapportées à \(Re_{ref} = 7 * 10^6\). Elles représentent le rapport des pertes relatives transposables aux pertes relatives totales (\(1 – \eta_{hopt}\)) au point de rendement hydraulique optimal, au nombre de Reynolds de référence \(Re_{ref} = 7 * 10^6\), pour les différents types de machines à réaction (voir annexe F du CEI60193[3]).
Voici la nomenclature du CEI définissant les variables pour calculer l'effet d'échelle :
\(Re=\frac{D U}{\nu}\)
\(V=\frac{\delta}{1-\eta_h}\)
\(\delta_{ns}=(1-\eta_h)-\delta=(1-\eta_h)*(1-V)\)
\(1-\eta_h=\delta+\delta_{ns}\)
La méthode à être mise en place repose sur une première transposition des résultats d'essai modèle à un même Reynolds. On pourra ensuite faire la transposition au prototype qui lui aussi est à un Reynolds constant.
Lors de l'essai en choisissant une vitesse de rotation constante pour tous les points de mesure, on peut éviter cette étape.
Méthode : Méthode de calcul de la transposition CEI
Formulation générale
On doit toujours se ramener au Reynolds de référence pour appliquer le bon ratio des pertes non transposables sur les pertes totales ; car ce ratio, Vref, y est connu par définition.
Dans un premier temps, on exprime la variation de rendement pour un même point de fonctionnement considéré à 2 Reynolds différents.
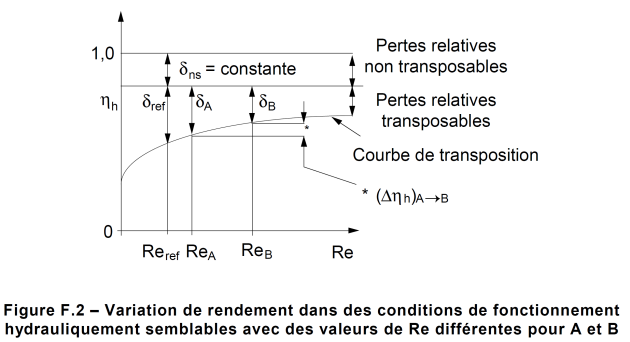
Soient 2 conditions hydrauliques, A et B, représentant le même point de fonctionnement (ned,Qed) mais à 2 nombres de Reynolds différents et dont on veut calculer la variation de rendement.
Si on considère les pertes transposables en chaque condition comparées à la perte au Reynolds de référence.
La norme CEI60193[3] nous définit les relations suivantes :
\(\frac{\delta_A}{\delta_{ref}}=\left(\frac{Re_{ref}}{Re_A}\right)^{0,16}\) et \(\frac{\delta_B}{\delta_{ref}}=\left(\frac{Re_{ref}}{Re_B}\right)^{0,16}\)
sachant que : \((\Delta \eta_h)_{A \rightarrow B}= \eta_B-\eta_A=(1-\eta_A)-(1-\eta_B)=\delta_A-\delta_B\)
\((\Delta \eta_h)_{A \rightarrow B}=\delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{A}}\right)^{0,16}-\left(\frac{Re_{ref}}{Re_{B}}\right)^{0,16}\right]\)
Formulation pour le point de meilleur rendement
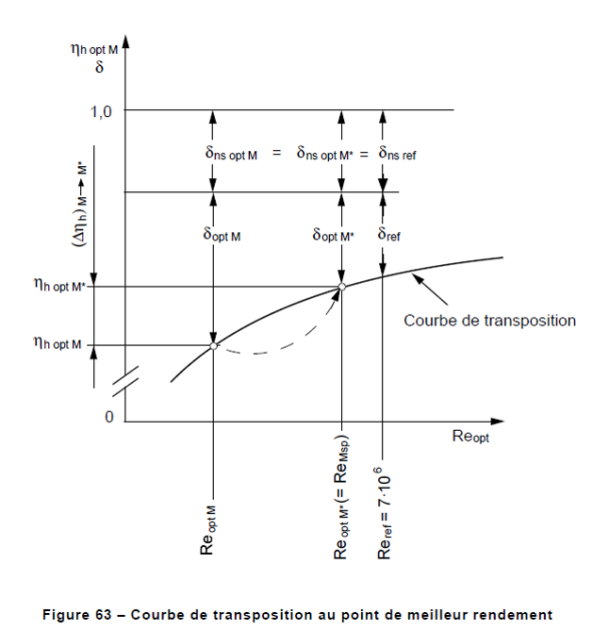
On applique maintenant cette relation avec le point de meilleur rendement entre sa condition de mesure et la condition au Reynolds de référence :
\(\frac{\delta_{optM}}{\delta_{ref}}=\left(\frac{Re_{ref}}{Re_{optM}}\right)^{0,16}\)
\(V_{ref}=\frac{\delta_{ref}}{\delta_{ref}+\delta_{nsoptM}}\)
\(\delta_{optM}+\delta_{nsoptM} = 1-\eta_{hoptM}\)
Toutefois, lors de la mesure sur modèle, certaines valeurs sont inconnues :
\(\delta_{optM}\) représente les pertes relatives transposables au point de meilleur rendement modèle, au Reynolds de l'essai modèle pour ce point.
\(\delta_{ref}\) représente les pertes relatives transposables au point de meilleur rendement, au Reynolds de référence imposé par le CEI soit 7*106 .
\(\delta_{nsoptM}\) représente les pertes relatives fixes au point de meilleur rendement modèle, pour n'importe quel Reynolds.
\((\Delta \eta_h)_{optM \rightarrow ref}=(1-\eta_{optM})-(1-\eta_{ref})=\delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{optM}}\right)^{0,16}-1\right]\)
\((1-\eta_{optM})=\delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{optM}}\right)^{0,16}-1\right] + (1-\eta_{ref})\)
\((1-\eta_{optM})= \delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{optM}}\right)^{0,16}-1\right] + \frac{\delta_{ref}}{V_{ref}}\)
\(\delta_{ref}=\frac{1-\eta_{optM}}{\left[ \left(\frac{Re_{ref}}{Re_{optM}}\right)^{0,16}+\frac{1-V_{ref}}{V_{ref}}\right] }\)
et quand les rendements sur modèle ont été rapportés à un nombre de Reynolds constant \(Re_M*\) :
\((\Delta \eta_h)_{M* \rightarrow P}=\delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{M*}}\right)^{0,16}-\left(\frac{Re_{ref}}{Re_{p}}\right)^{0,16}\right]\)
et c'est la même valeur pour tout l'essai.
Si l'essai modèle n'est pas à Reynolds constant on utilise alors :
\((\Delta \eta_h)_{M \rightarrow P}=\delta_{ref}\left[ \left(\frac{Re_{ref}}{Re_{M}}\right)^{0,16}-\left(\frac{Re_{ref}}{Re_{p}}\right)^{0,16}\right]\)
à calculer pour chaque point.
Une pratique élégante serait de toujours présenter les résultats d'essai modèle normalisés au Reynolds de référence