Champ de pression généré par un tourbillon libre

FondamentalCalcul de la pression résultant du champ d'accélération dans un tourbillon libre

Dans un tourbillon libre, la circulation est constante et conditionne la pression. Elle exprime aussi la conservation du moment cinétique. De ce fait, pour exister, le moment cinétique est transporté par une vitesse radiale. L'absence d'un écoulement radial dans un tourbillon confirme que le tourbillon est un tourbillon forcé.

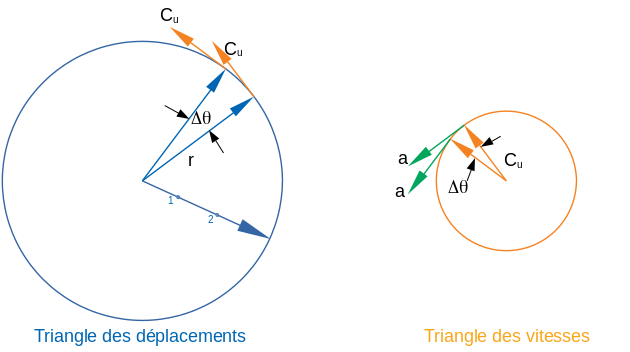
Similitude graphique des déplacements et vitessesInformations[1]

Considérons deux points 1 et 2, dans un tourbillon libre :

Le tourbillon libre se caractérise par une circulation constate : \(\Gamma = r\ C_u\) dans le domaine du tourbillon.

Sachant que \(C_u = r \ \omega\), \(\Gamma = r\ r\ \omega\) et donc \(\omega = \frac{\Gamma}{r^2}\)

La pression s'exprime :

\(p=\int_{r_1}^{r_2} \rho \ r \ \omega^2 \ dr\)

\(p=\int \rho \ r \left( \frac{\Gamma^2}{r^4}\right) dr= \frac{-\rho\Gamma^2}{2r^2}+ Constante\)

\(p_2-p_1 = \frac{\rho\Gamma^2}{2r_1^2}-\frac{\rho\Gamma^2}{2r_2^2}\)

\(p_2-p_1 = \frac{\rho\Gamma^2}{2}\left( \frac{1}{r_1^2}-\frac{1}{r_2^2}\right)=\frac{\rho}{2}(C_{u1}^2-C_{u2}^2)\)

Cette dernière expression nous donne la pression dans le tourbillon libre.

FondamentalPoussée axiale résultant du champ de pression généré par un tourbillon libre

On observe que la variation de pression est directement liée à la vitesse tangentielle du fluide peu importe s'il s'agit d'un tourbillon libre ou forcé. Néanmoins, la vitesse tangentielle est très différente selon le tourbillon et donc la pression sera aussi très différente pour les deux types de tourbillon.

On peut intégrer cette pression sur la surface du disque considérée pour trouver une poussée axiale.

Pour le tourbillon libre on obtient :

F = ∫ p dA F = ∫ r 1 r 2 ∫ 0 2 π r ( − ρ Γ 2 2 r 2 + Constante ) dr d θ = ∫ r 1 r 2 ( − ρ Γ 2 2 r 2 + Constante ) 2 π r dr F = π ρ Γ 2 ( ln r 1 − ln r 2 ) + Constante ∗ π ( r 2 2 − r 1 2 ) avec Constante = p i + ρ Γ 2 2 r i 2 {F} = int p dA newline F = int from{r_1} to{r_2} int from{0} to{2 %pi r} left ( {-%rho {%GAMMA } ^2} over { 2 {r} ^2} +Constante right) dr d %theta =int from{r_1} to{r_2} left ( {-%rho {%GAMMA} ^2} over { 2 {r} ^2} +Constante right)2 %pi {r} dr newline {F} = %pi %rho {%GAMMA} ^2 left ( ln {r_1} - ln {r_2} right )+Constante* %pi ( {r_2} ^2- {r_1} ^2 ) newline avec Constante = p_i+ { %rho {%GAMMA} ^2 } over {2 {r_i} ^2}

ExempleCalcul des efforts axiaux sur un disque dans un champ de pression d'un tourbillon libre

Deux cas se présentent pour le tourbillon libre, la vitesse tangentielle est imposée au diamètre interne ou au diamètre externe.

Cas1 - Vitesse angulaire imposée au rayon interne

Imaginons un espace annulaire entre deux disques. Au diamètre intérieur de cet anneau, il y a un croisillon solidaire des disques.

L'espace annulaire est dimensionné entre 30 et 70 mm de rayon et la structure tourne à 5500 tpm[2]. Il y a un écoulement radial, entre ces deux rayons, qui transporte le moment cinétique.

Étant donné une pression mesurée à 100 kPa au rayon de 30 mm, calculons la pression au rayon 70 mm.

Tourbillon libre entre deux disques avec vitesse imposée au diamètre intéreurInformations[3]

La vitesse angulaire est : \(\omega = 5500 \ tpm * \frac {2 \pi \ radians}{1 tour}* \frac {1 min}{60 \ secondes}= 576\ radians / s\)

\(C_u = r \ \omega\)

\(C_{u30}= 0,03 * 576 = 17,3 \ m/s\)

On calcule maintenant la circulation qui caractérise le tourbillon libre dans l'espace annulaire entre les deux disques :

\(\Gamma = r*C_u = 0,03*17,3 = 0,52 \ m²/s\)

Ce qui nous permet de calculer la vitesse au rayon 70 mm : \(C_{u70}=0,52/0,07 = 7,4 \ m/s\)

Puis la pression :

\(p_{70} - p_{30} = \frac{\rho }{2} ( C_{u30}^2-C_{u70}^2) = \frac{1000 }{2} ( 17,3^2-7,4^2) = 122,3 \ kPa\)

\(p_{70}=122,3+100 \ kPa=222,3 \ kPa\)

Calculons maintenant l'effort sur la face horizontale d'un disque.

On calcule la constante d'intégration au rayon 30 mm :

\(Constante = 100000+\frac{1000 *0,052^2}{2*0,03^2}= 249278 \ Pa\)

Maintenant, la force sur le disque dans ce champ d'accélération.

\(F=\pi *1000*0,052^2*(\ln 0,03-\ln 0,07) + 249278 * \pi *(0,07^2-0,03^2)=2417 \ N\)

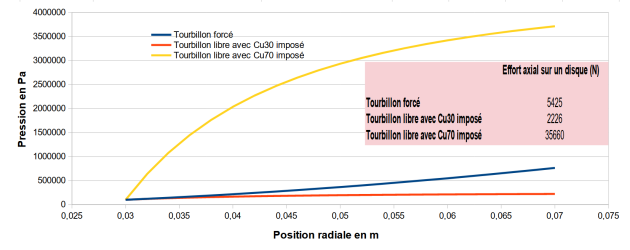
On observe que pour le chargement décrit, l'effort est plus important dans le cas du tourbillon forcé.

Cas 2 - Vitesse angulaire imposée au rayon externe

Imaginons un espace annulaire entre deux disques. Au diamètre extérieur de cet anneau, il y a un croisillon solidaire des disques.

L'espace annulaire est dimensionné entre 30 et 70 mm de rayon et la structure tourne à 5500 tpm[2]. Il y a un écoulement radial entre ces deux rayons qui transporte le moment cinétique.

Tourbillon libre entre deux disques avec vitesse imposée au diamètre intéreurInformations[4]

Étant donné une pression mesurée à 100 kPa au rayon de 30 mm, calculons la pression dans l'espace annulaire entre les deux disques.

La vitesse tangentielle au diamètre extérieur :

\(C_{u70}= 0,07 * 576 = 40,3 \ m/s\)

Ce qui donne une circulation de :

\(\Gamma = r*C_u = 0,07*40,3 = 2.82 \ m²/s\)

La vitesse tangentielle au diamètre intérieur est :

\(C_{u30}= \frac{\Gamma}{r_{30}}=94,1 \ m/s\)

comme pour le cas 1 la pression se calcule :

\(p_{70} - p_{30} = \frac{\rho }{2} ( C_{u30}^2-C_{u70}^2)\)

\(p_{70}=3712\ kPa\) ce qui est nettement supérieur aux autres cas calculés.

Voici un graphique montrant les pressions comparées résultants du tourbillon forcé et des deux cas de tourbillon libre.

Avec une même pression au diamètre intérieur, comparaison de la pression selon le type de tourbillonInformations[5]

On peut retrouver le tableur menant à ce graphique ici.