La pression due à la gravité - L'hydrostatique [Turbines hydrauliques

La pression due à la gravité - L'hydrostatique

Fondamental :

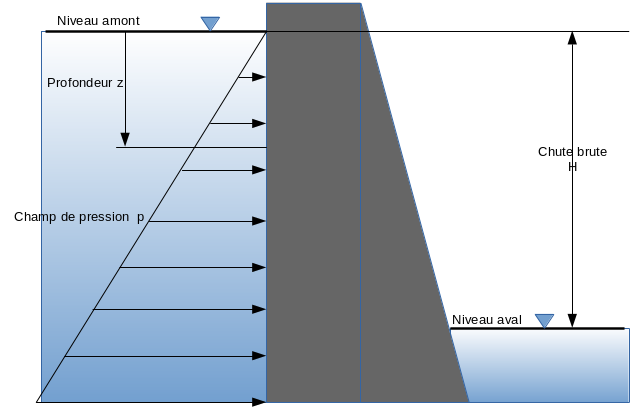
À une profondeur z depuis la surface, la pression hydrostatique pour un fluide incompressible s'exprime :

$p = ρ g z$

$Pa = {kg/m^3}× {m/s^2}× m = N/m^2$

La pression peut aussi être vue comme une énergie massique potentielle :

$E = \frac{p}{ρ} = g * z$

$J/kg = Pa / (kg/m^3) = m^2 /s^2$

Pour l'énergie potentielle, l'axe $z$ s'exprime positif vers le haut.

Dans la pratique, l'usage est de présenter le niveau d'énergie par la variable $h$ en mce^[2].

Ainsi : $h = E/g$

Complément : Comparaison de la pression entre 2 points immergés à des altitudes différentes

Soit $z_a$ et $z_b$ les profondeurs respectives de deux points A et B.

Soir $p_{ref}$ la pression à la surface.

Au point A on aura la pression $p_a=\rho g z_a + p_{ref}$ et

au point B on aura la pression $p_b=\rho g z_b+p_{ref}$

On peut donc exprimer la pression de l'un par rapport à l'autre si on connait les altitudes de chacun.

Ainsi $p_b - p_a = \rho g (z_b-z_a)$ nous donne :

$p_b = \rho g (z_b-z_a) + p_a$

$p_a = \rho g (z_a-z_b) + p_b$

Connaissant la pression en un point, on peut en déduire la pression à un autre point si on connait la différence d'altitude entre ces deux points.

Les conditions sous entendues pour assurer la validités de ces équations sont :

Le fluide est au repos.
La masse volumique $\rho$ du fluide et le champ de la gravité $g$ sont constants partout.
Les deux points sont dans le même volume, ils ne sont pas séparés par une paroi.
L'axe $z$ est positif vers le bas.

Remarque : Cote par rapport au niveau de la mer

Le niveau d'eau est toujours une position relative, on l'exprime souvent par rapport au niveau de la mer. Il correspond aussi à un niveau d'énergie. On utilise parfois l'expression mce^[2] pour le dimensionner, cela correspond à mètre de colonne d'eau, cet usage fait du niveau d'eau une expression d'un niveau d'énergie. Sur la coupe du barrage, la différence entre les niveaux amont et aval représente une énergie disponible, exprimée en mce cela correspond à la définition de la chute brute.

Fondamental : Effort sur une surface verticale dû à la pression hydrostatique

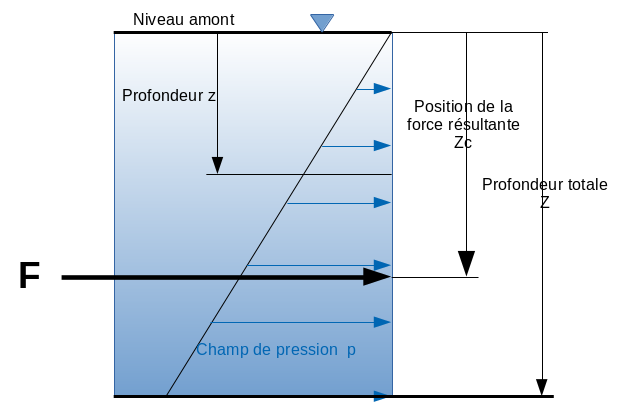
Effort de pression sur une paroi verticale | Informations^[3]

Il s'agit ici de calculer la force résultant de la pression hydrostatique sur la face verticale d'une paroi. D'abord, on exprime cette force comme étant l'intégrale de la pression sur cette surface puis on la représente constante sur toute la largeur ($L_p$) du barrage :

\begin{matrix} F = \int p dA \\ \frac{F}{L_{p}} = \int_{0}^{Z} ρ g z dz \\ \frac{F}{L_{p}} = \frac{ρ g Z^{2}}{2} \end{matrix}

Maintenant pour le couple de renversement causé par la force résultant du champ de pression :

\begin{matrix} M = F Z_{c} = \int p z dA \\ \frac{F}{L_{p}} Z_{c} = \int_{0}^{Z} ρ g z^{2} dz \\ \frac{F}{L_{p}} Z_{c} = \frac{ρ g Z^{3}}{3} \end{matrix}

La position de la force qui cause ce moment est :

Z_{c} = \frac{2}{3} Z

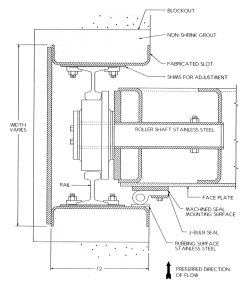
Exemple : Calcul des charges sur les roues d'une vanne wagon

Vannes wagons et leurs mécanismes de manutention | Informations^[4]

Les vannes wagon sont souvent utilisées à la prise d'eau ou au déversoir. Elles sont rectangulaires et s'insèrent dans des rainures qui sont équipées de rails. Il y a des roues qui transmettent les charges créées par la pression. Elles se manœuvrent en environ 5 minutes et sont soumises à de relativement faibles pressions.

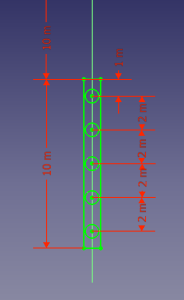
Détail de la rainure d'une vanne wagon | Informations^[5]

Supposons une prise d'eau équipée d'une vanne wagon rectangulaire exposée à la pression amont sur 10 m de haut par 8 m de large.

Elle est équipée de 5 paires de roues également distribuées en hauteur. Le haut de la vanne est, en position fermée, situé à 10 m sous le niveau amont.

Calculons la charge sur chacune des roues.

Du paragraphe précédent on peut exprimer la force en Newton sur la section 1 qui va de 10 à 12 m de profondeur par : $F=L_p \rho g \frac{(z_{12}^2-z_{10}^2)}{2}$

On peut exprimer la force en tonne $F_T=\frac{F}{1000 g}$ on trouve donc :

$F_T=\cfrac{L_p \rho g \frac{(z_{12}^2-z_{10}^2)}{2}}{1000 g} = 8 * \frac{12^2-10^2}{2} = 176 \ T$ pour la section soit $88 \ T$ par roue.

Pour la section 2 entre 12 et 14 m de profondeur : $F_T=8 * \frac{14^2-12^2}{2} = 208 \ T$ soit $104 \ T$ par roue.

Pour la section 3 entre 14 et 16 m de profondeur : $F_T=8 * \frac{16^2-14^2}{2} = 240 \ T$ soit $120 \ T$ par roue.

Pour la section 4 entre 16 et 18 m de profondeur : $F_T=8 * \frac{18^2-16^2}{2} = 272 \ T$ soit $136 \ T$ par roue.

Pour la section 5 entre 18 et 20 m de profondeur : $F_T=8 * \frac{20^2-18^2}{2} = 304 \ T$ soit $152 \ T$ par roue.

Pour une charge totale sur la vanne de $1200 \ T$.