Champ de pression généré par un tourbillon forcé
Fondamental :
Dans une rotation, la vitesse angulaire constante (\(\omega\)) génère un champ d'accélération (\(a\)) qui conditionne la pression.
La variation de la position angulaire dans le temps nous donne : \(\omega = \frac{d \theta}{d t} =\frac{Cu}{r}\)
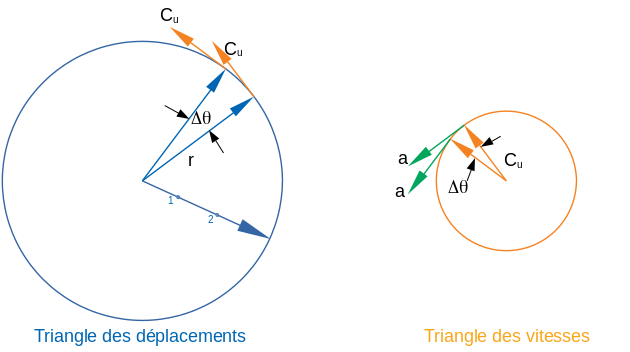
Pour un intervalle de temps donné, on obtient une similitude du triangle des déplacements avec celui des vitesses.
Ainsi, le long de la trajectoire circulaire, pour un intervalle de temps infinitésimal la distance parcourue peut s'exprimer : \(r d \theta = Cu dt\)
et simultanément, la variation des vitesses s'exprime sur la même variation angulaire : \(Cu \ d \theta = a \ dt\)
En éliminant \(d \theta\) de ces deux équations, on obtient :
\(a=\frac{Cu^2}{r}=r\omega^2\)
\(F={\displaystyle \int^{Vol} \rho a \ d{Vol} = \int_{r_1}^{r_2} \rho r \omega^2 \ dr \ dA}\)
\(p = \displaystyle \int \rho r \omega^2 \ dr= \frac {\rho r^2 \omega^2}{2} + Constante\)
\(p_2-p_1=\frac{\rho(r_2^2-r_1^2)\omega^2}{2}=\frac{\rho}{2}(Cu_2^2-Cu_1^2)\)
Cette dernière expression nous donne la pression dans un tourbillon forcé. Connaissant la pression en un point et la vitesse angulaire, on peut calculer la pression à un autre point en fonction des coordonnées radiales de ces deux points.
Fondamental : Poussée axiale résultant du champ de pression généré par un tourbillon forcé
On observe que la variation de pression est directement liée à la vitesse tangentielle du fluide peu importe s'il s'agit d'un tourbillon libre ou forcé. Néanmoins, la vitesse tangentielle est très différente selon le tourbillon et donc la pression sera aussi très différente pour les deux types de tourbillon.
On peut intégrer cette pression sur la surface du disque considérée pour trouver une poussée axiale.
Pour le tourbillon forcé, la force axiale exercée sur le disque est :
\(F=\displaystyle\int p \ dA= \int_{r_1}^{r_2} \int_{0}^{2\pi r} \left( \rho \frac{r^2}{2} \omega^2 + Constante \right)dr \ d\theta\)
\(F=\displaystyle \int_{r_1}^{r_2}\left( \rho \frac{r^2}{2} \omega^2*2 \pi r +Constante *2 \pi r \right) dr\)
\(F= \pi \rho \omega^2 \frac{1}{4}(r_2^4-r_1^4)+Constante*\pi(r_2^4-r_1^4)\)
avec \(Constante = p_i - \frac{\rho r^2 \omega^2}{2}\)
Exemple : Calcul des efforts axiaux sur un disque entraînant un fluide en rotation
Imaginons une paire de disques qui entraînent un fluide à l'aide d'ailettes radiales dimensionnées entre 30 et 70 mm de rayon et tournant à 5500 tpm[2].
Étant donné une pression mesurée à 100 kPa au rayon de 30 mm, calculons la pression au rayon 70 mm.
Calcul de la pression
On commence par calculer les vitesses tangentielles aux deux rayons d'intérêt.
La vitesse angulaire est : \(\omega = 5500 \ tpm * \frac {2 \pi \ radians}{1 tour}* \frac {1 min}{60 \ secondes}= 576\ radians / s\)
On est dans le cas du tourbillon forcé. La vitesse tangentielle \(C_u\) s'exprime par rapport à la vitesse angulaire\( \omega\).
\(Cu = r \ \omega\)
\(Cu_{30}= 0,03 * 576 = 17,3 \ m/s\)
\(Cu_{70}= 0,07 * 576 = 40,3 \ m/s\)
On a vu précédemment que :
\(p_{70} - p_{30} = \frac{\rho }{2} ( Cu_{70}^2-Cu_{30}^2) = \frac{1000 }{2} ( 40,3^2-17,3^2) = 662 \ kPa\)
\(p_{70} = (662 + 100) \ kpa = 762 \ kPa\)
Calculons maintenant l'effort sur la face horizontale d'un disque.
Calcul de la force axiale
La constante d'intégration pour notre problème est :
\(Constante = 100000- \frac{1000 *0,03^2 *576^2}{2}= -49300 \ Pa\)
Maintenant, la force sur le disque dans ce champ d'accélération.
\(F=\pi *1000* \frac{576^2}{4}(0.07^4-0,03^4)-49300*\pi*(0,07^2-0,03^2)=5425 \ N\)
Ici, on a fait abstraction de la section des ailettes qui réduisent la surface du disque et donc la force.
On doit observer, qu'un écoulement radial peut se superposer au phénomène et il peut exister dans les deux directions, sans perturber fondamentalement le phénomène analysé ici.