La vitesse spécifique [Turbines hydrauliques

La vitesse spécifique

Expression de la similitude en fonction des paramètres hydrauliques

Le retour au triangle de vitesse nous amène les conditions de conservation des angles dans le repère tournant : la roue. Entre 2 roues géométriquement similaires, en chaque point la vitesse relative $W$ doit être en similitude. Cela nous amène à une expression de la condition de conservation des angles :

$(Cu-U)/Cm$ exprime le même triangle de vitesse entre 2 points sur 2 roues similaires.

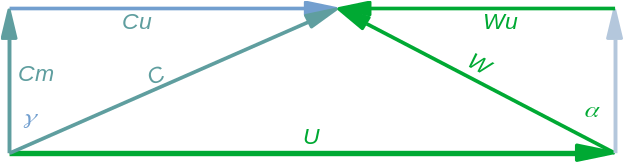
Triangle de vitesse dans une roue | Informations^[1]

Donc,

Les ratios $Cu/Cm$ et $U/Cm$ doivent être conservés entre les 2 turbines similaires.
On observe que $Cu$ et $Cm$ sont liées entre elles par une constante et à $\sqrt H$ par la relation de Combe-Rateau : $Cu=Cm * tan(\gamma) = constante * \sqrt{H}$
Alors que de façon indépendante $U$ est lié à $\omega$ et à la géométrie par : $U = \omega \frac{D}{2}$

Et $Cm$ est liée à la géométrie par:

$C_m=\frac {Q} {A}=\frac{Q}{\pi \left({\frac{D}{2}}^2\right)}=constante*\sqrt{H}$

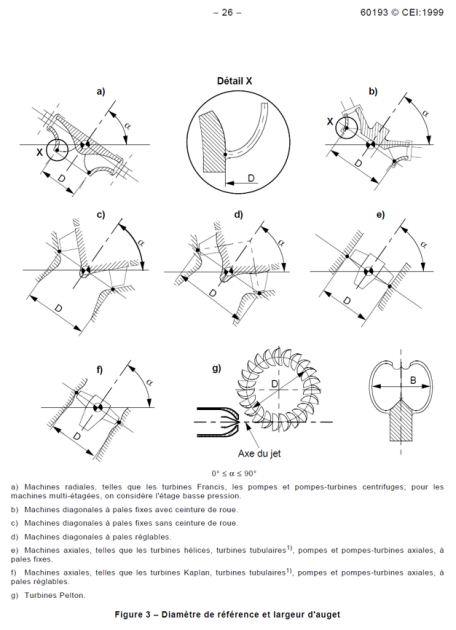
On utilise habituellement, le diamètre $D$ à la sortie des aubes en mode turbine comme référence de dimension.

Le chiffre de référence pour la dimension de la turbine | Informations^[2]

Entre 2 machines, considérons le triangle des vitesses à la sortie et au diamètre maximum :

$\begin{matrix} D'une part: \\ \frac{Q'}{Q''} = \frac{C_{m}' π {(\frac{D'}{2})}^{2}}{C_{m}'' π {(\frac{D''}{2})}^{2}} = Q^{*} = \sqrt{H^{*}} L^{*2} \to L^{*} = \sqrt{\frac{Q^{*}}{\sqrt{H^{*}}}} \\ D'autre part: \\ \frac{U' C_{m}''}{C_{m}' U''} = \frac{n' D'}{n'' D''} \frac{1}{\sqrt{H^{*}}} = \frac{n^{*} L^{*}}{\sqrt{H^{*}}} = constante = n^{*} \frac{\sqrt{Q^{*}}}{H^{*0,75}} \end{matrix}$

Dans cette dernière équation en imposant le ratio des dimensions $L^*$ comme étant une fonction du débit et de la chute, on contraint le respect du triangle des vitesses.

Ce qui nous amène à la définition de la vitesse spécifique.

Définition : La vitesse spécifique

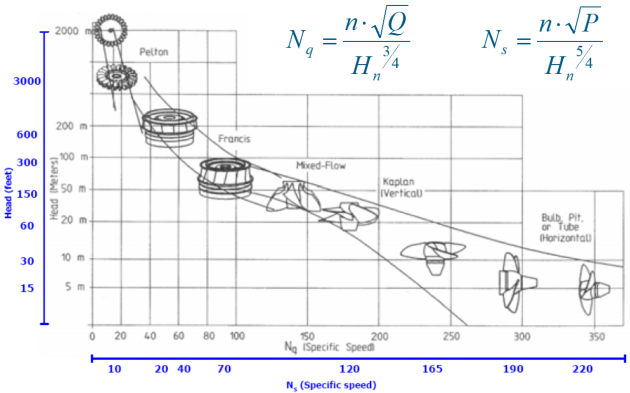
Selon CEI60193, la définition de la vitesse spécifique est :

$n_{QE} = \frac{n \sqrt{Q}}{E^{0,75}}$ qui est une valeur adimensionnelle. Elle correspond à la vitesse de rotation en tps de la turbine pour une énergie de 1 Joule et un débit de 1 m³/s.

La vitesse spécifique permet de classer les turbines sur la base de leur chute, débit et vitesse de rotation. Pour une turbine donnée, elle se calcule généralement au point de pleine charge mais idéalement au point de meilleur rendement.
Pour un angle d'incidence donné ($\alpha$), la vitesse décroît avec l'augmentation de la chute.
Elle sert à bâtir des statistiques pour faire le choix d'une machine.
Peut s'exprimer aussi en fonction de la puissance : $n_{s} = \frac{n_{tpm} \sqrt{P_{m}}}{H^{1,25}}$
Il existe plusieurs formulations dimensionnelles. Attention aux unités.
- Parfois, le point de fonctionnement considéré n'est pas celui de meilleur rendement, cela peut être la pleine charge ou autre chose.
- P peut s'exprimer en kW, HP (746 watts), CV (736 watts).
- H peut s'exprimer en m ou en pied.
- n peut s'exprimer en tpm ou tps.

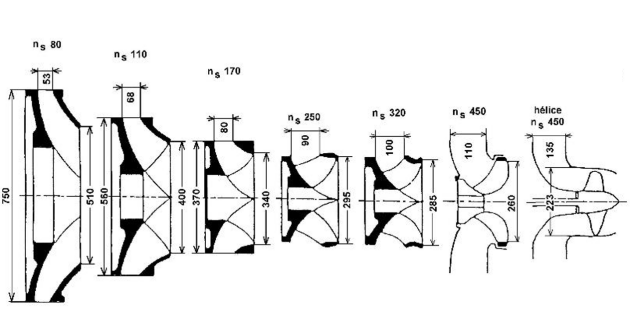
Complément : Évolution de la forme des turbines en fonction de la vitesse spécifique

La vitesse spécifique permet de suivre l'évolution de certains paramètres:

Forme
Rendement
Cavitation

Évolution de la forme des turbines avec la vitesse spécifique et la chute | Informations^[3]

Évolution de la forme de radial à axial avec la vitesse spécifique | Informations^[4]

On peut expliquer l'évolution des formes de la façon suivante :

Le débit à l'entrée peut s'exprimer : $Q=A_1 C_{m1} = \pi b_d D_1 C_{m1}$

La vitesse de rotation en tps peut s'exprimer : $n_{tps} = \frac{U_1}{D_1\pi}$

Ce qui nous amène à la réécriture de la vitesse spécifique de la façon suivante :

$n_{QE} = n_{tps}\frac{\sqrt{Q}}{E^{{3}/{4}}}=\frac{U_1}{D_1\pi}\frac{\sqrt{\pi b_d D_1 C_{m1}}}{E^{{3}/{4}}}$

En exprimant le tout sous le radical on obtient :

$n_{QE} =\sqrt{\frac{1}{\pi}\left(\frac{b_d}{D_1}\right)U_1^2C_{m1}E^{-3/2}}$

Pour $D_1$ et $E$ donnés, on connait les valeurs de $U_1$ et $C_{m1}$, seul $b_d$ reste variable, on peut donc conclure que la vitesse spécifique croît avec le ratio $\frac{b_d}{D_1}$, ce que les figures précédentes nous permettent d'observer.

Comme au sommet de rendement $C_{u2}=0$ et donc $E=U_1 C_{u1}$ et sachant que $\tan {\gamma_1}=C_{u1} / C_{m1}$ :

$n_{QE} =\sqrt{\frac{1}{\pi}\left(\frac{b_d}{D_1}\right)\frac{U_1}{\tan {\gamma_1}} E^{-1/2}}=\sqrt{\frac{D_1}{2\pi}\left(\frac{b_d}{D_1}\right)\frac{\omega}{\tan {\gamma_1}} E^{-1/2}}=\sqrt{\frac{1}{2\pi}b_d\frac{\omega}{\tan {\gamma_1}} E^{-1/2}}$

Pour $\gamma_1$, $\omega$ et $E$ donnés, seul $b_d$ reste variable, on peut donc conclure que la vitesse spécifique croît avec la hauteur du distributeur $b_d$ ,ce que les figures précédentes nous permettent d'observer.

Remarque :

Le système de la vitesse spécifique est unidimensionnel et donc très simple, faute d'information sur le comportement en détail, il permet néanmoins de classifier les turbines. Toutefois, pour l'hydraulicien, il manque de l'information. En effet, comme on l'a vu, la turbine répond en performance à deux intrants : le débit et l'énergie. En plus, sa configuration géométrique est basée sur ces 2 critères. On a donc besoin d'un système à 2 dimensions pour permettre à l'hydraulicien de mieux analyser la turbine pour optimiser son déploiement.