Le nombre de cavitation: définition et effet macroscopique sur le comportement de la turbine
Bien avant la théorie des germes, la limite imposée par la tension de vapeur dans un environnement réel, c'est-à-dire saturé en germes, a été observée.
On observe l'apparition de la cavitation lorsque la pression absolue au point d'intérêt atteint la tension de vapeur qui est légèrement au dessus de zéro. Donc la pression ambiante absolue moins la tension de vapeur représente une valeur significative pour évaluer le danger de cavitation. C'est ce qu'on appelle le NPSH, Net Positive Suction Head ou si exprimé en terme d'énergie c'est le NPSE, Net Positive Specific Energy.
\(\frac{NPSE}{g}=NPSH= h_{absolue} - h_v \), le tout exprimé ici en mce.
Pour comparer deux machines similaires fonctionnant au même point, donc avec les mêmes chiffres de similitude, on peut écrire :
\(\frac{NPSH'}{NPSH''}=\frac{H'}{H''}\)
Si les deux machines sont en similitude de Froude, ce ratio caractérisera tout le circuit de la turbine. Par contre, si on est en similitude de Combe-Rateau, ce ratio ne tient qu'à une position donnée dans le circuit. Cette position d'intérêt est choisie pour être la plus susceptible de caviter.
Dans une turbine hydraulique, la pression statique la plus faible est obtenue à la roue où on trouve une vitesse élevée. Généralement c'est près du bas des aubes sur les Francis et à l'axe roue sur les Kaplan.
Définition : Le nombre de cavitation: critère de similitude pour la cavitation
Pour un point géométrique localisé significativement on définit généralement :
\(\sigma = \frac{\frac{p_{absolue}-p_v}{\rho}}{E}=\frac{NPSE}{E}=\frac{NPSH}{H}\)
La détermination du NPSE ou NPSH est expliquée par la norme CEI60193 et considérant une turbine prototype, on peut écrire :
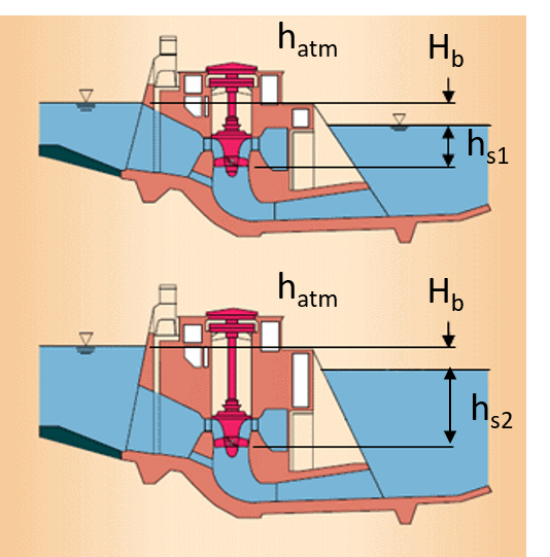
\(NPSE= \frac{p_{atm}-p_v}{\rho} + gh_{faspi}-gh_s\)
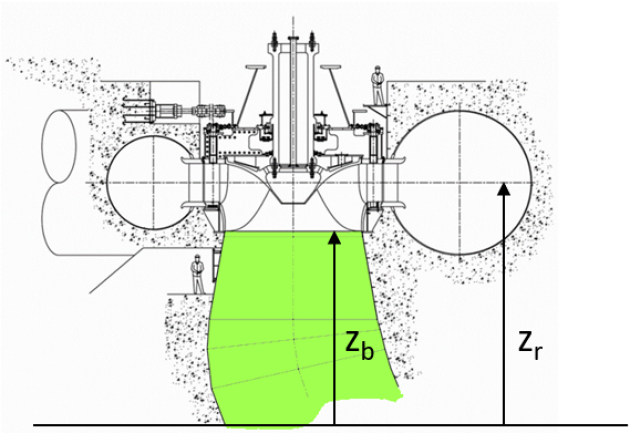
où la hauteur de sustentation est définie par rapport aux altitudes du point considéré de la roue et du niveau aval :
\(h_s=z_r-z_{aval}\)
et donc :
\(\sigma=\frac{h_{atm}+h_{faspi}-h_s-h_v}{H}\)
On observe que le NPSE tient compte d'une augmentation de pression due à l'énergie cinétique perdue à la sortie de l'aspirateur hfaspi . Quand cette énergie est basée sur le calcul d'une vitesse moyenne débitante, elle ne représente en réalité qu'une fraction de la perte réelle. Elle est généralement faible.
Il faut faire attention au choix du point significatif. Si sur une Kaplan on choisit généralement l'axe de la roue, sur une Francis cela peut être l'axe du distributeur ou le bas des aubes. Selon le choix, la valeur du σ ne sera pas la même.
Contrairement aux autres chiffres de similitude, le nombre de cavitation n'est pas un rapport de 2 forces. C'est le rapport de la pression absolue moins la tension vapeur à l'énergie hydraulique, le tout exprimé dans des unités cohérentes pour obtenir un chiffre adimensionnel.
Complément :
Sur les turbines Francis de grande dimension sous faible chute, la différence d'altitude entre l'axe du distributeur (ou axe roue) peut être significatif. Il est alors d'usage de prendre comme point significatif le bas des aubes, c'est-à-dire la sortie de la roue.
\(\sigma_{zb}=\sigma_{zr}+\frac{z_r-z_b}{H}\)
Fondamental : Effet macroscopique de la cavitation sur la turbine
Pour une installation donnée, un σ élevé représente un enfoncement élevé.
En faisant varier le σ on simule une variété d'enfoncements et on peut en observer les conséquences sur le comportement:
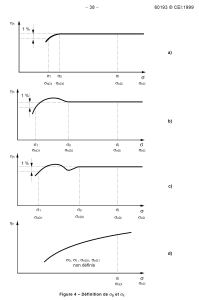
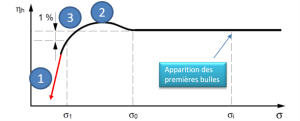
À partir d'un σ critique on observe une chute des performances (rendement et puissance).
Dans certaines circonstances on observe de légères augmentations de rendement.
Lors de l'essai modèle, la procédure de modification du σ est assez simple. Il s'agit de modifier la pression de la boucle sans changer les autres paramètres ( chute, débit), donc vitesses constantes pour la pompe et la turbine. La pression de la boucle est l'effet d'une pompe à vide ou d'un compresseur débouchant au sommet de la cuve aval.
Fondamental : Comment la cavitation perturbe le comportement de la turbine
La cavitation se produisant à la sortie de la roue peut à la limite faire en sorte que la tension de vapeur soit atteinte. La roue est alors isolée du niveau aval et une diminution du σ revient à une diminution de la chute.
On observe parfois une augmentation de rendement. Cela peut s'expliquer par la vapeur qui diminue la friction avec les surfaces solides, on aurait alors une augmentation du rendement. Un endroit susceptible est le labyrinthe.
La vapeur peut obstruer certains passages et pousser l'écoulement ailleurs. Il peut en résulter un meilleur ou un pire rendement.