Turbines hydrauliques - Capsules théoriques

Aux faibles sigmas, la chute de rendement observée peut s'expliquer par la diminution de la chute vue par la roue, plus précisément de la chute interne.

En effet, lorsque le sigma diminue, c'est comme si l'axe roue montait entre le niveau amont et aval. Lorsque la cavitation à la sortie de la roue sature, la roue ne voit plus le niveau aval mais plutôt la tension de vapeur qui est constante. Dans ces circonstances, remonter la roue diminue la distance niveau amont - axe roue tout en conservant la tension de vapeur à la sortie de la roue. Il en résulte une diminution de la chute vue par la roue.

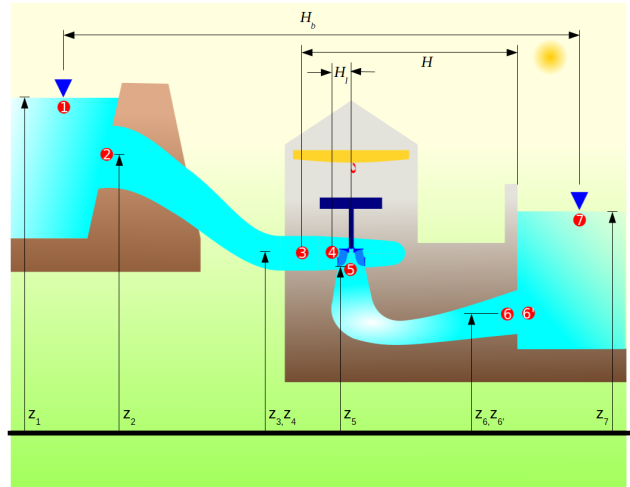
Considérons la figure suivante :

On a vu que la chute nette s'exprime entre les points 3 et 6 comme étant

\(H=\left(\frac{p_3}{\rho g} + g z_3 +\frac{\left({\frac{Q}{A_3}}\right)^2}{2 g}\right)-\left( \frac{p_6}{\rho g} + g z_6+\frac{\left({\frac{Q}{A_6}}\right)^2}{2 g}\right)\)

On note que dans tous les cas, peut importe l'altitude de la roue définie par \(z_5\) la chute nette n'est pas affectée.

Considérons l'altitude limite du sigma critique avec le cas \(a\) et le cas \(b\) est lui, saturé en cavitation, résultant respectivement des hauteurs de sustentation \(h_{sa}\) et \(h_{sb}\). Les indices \(3\) et \(5\) correspondent à l'entrée de la turbine et à la sortie de la roue.

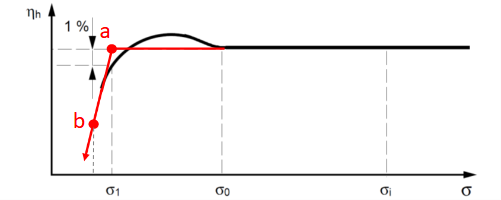
La variation du sigma est causée par une variation du niveau de la roue \(z_5\). La différence d'énergie entre le point \(3\) et le point \(5\) reste constante hors cavitation même lorsque le sigma varie. Regardons maintenant les cas lorsqu'il y a cavitation.

Considérons l'énergie locale en \(5\) pour le cas \(a\) :

\(h_{5a}= z_{5a}+\frac{p_{5a}}{\rho g}+\frac{v_5^2}{2 g}\)

On note que la vitesse au point \(5\) ne change pas avec l'altitude puisque que le débit est constant pour les cas \(a\) et \(b\).

Puisque qu'on est au sigma où la cassure de la courbe commence parce que la pression y est limitée à la tension de vapeur, l'énergie locale en \(5\) s'écrit maintenant :

\(h_{5a}= z_{5a}+h_v+\frac{v_5^2}{2 g}\)

Considérons l'énergie locale en \(5\) pour le cas \(b\) :

\(h_{5b}= z_{5b}+\frac{p_{5b}}{\rho g}+\frac{v_5^2}{2 g}\)

Le cas \(b\) est situé en pleine cavitation et la cavitation y est aussi limitée à la tension de vapeur.

\(h_{5b}= z_{5b}+h_v+\frac{v_5^2}{2 g}\)

On se rend compte que l'énergie en \(5\) varie lorsque le sigma est plus petit que le sigma critique.

Considérons l'énergie disponible à la roue \(H_{35}\)\(=h_3-h_{5}\)

Pour le cas \(a\) :

\(H_{35a}= h_3- z_{5a}+h_v+\frac{v_5^2}{2 g}\)

Pour le cas \(b\) :

\(H_{35b}= h_3- z_{5b}+h_v+\frac{v_5^2}{2 g}\)

La différence d'énergie disponible à la roue s'exprime donc :

\(H_{35b}-H_{35a}=z_{5a}-z_{5b}\)

Comme les hauteurs de sustentation \(h_{sa}=z_{5a}-z_7\) et \(h_{sb}=z_{5b}-z_7\)

\(H_{35b}-H_{35a} =h_{sa}-h_{sb}\)

Ce qui ramené à la chute nous donne une variation de rendement :

\(\Delta \eta_{a->b} =\frac{H_{3b}-H_{3a}}{H}=\frac{-h_{sb} + h_{sa}} {H}\)

Sachant que \(\sigma=\frac{h_{atm}+h_{faspi}-h_s-h_v }{H}\)

On a :

\(\Delta \sigma = \sigma_b- \sigma_a=\frac{-h_{sb} + h_{sa}} {H}\)

On obtient donc :

\(\color{red}\Delta \eta =\Delta \sigma\)

Donc, en condition de saturation en cavitation de sortie, la variation de rendement est égale à la variation de sigma. C'est une droite.