La cavitation et Bernoulli
La cavitation et Bernoulli
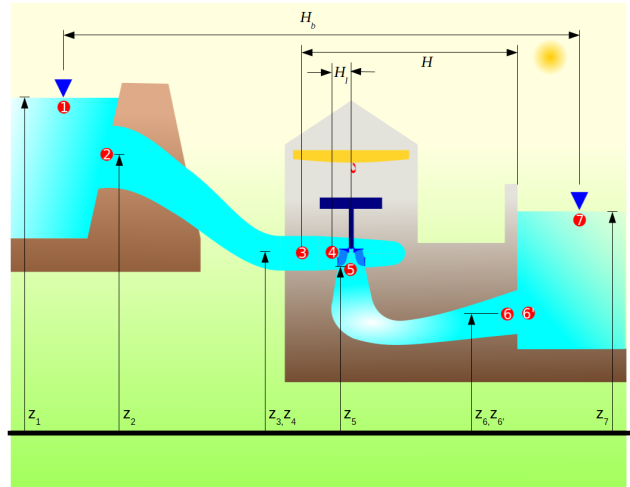
Considérons une turbine fonctionnant en régime permanent.
Au point 7, l'énergie locale s'exprime :
\(h_7=h_{atm}+z_7\)
Et comme on l'a vu dans le paragraphe Énergie locale et aux bornes :
\(h_{7}=h_{6'}\)
Sachant que \(h_{6'}=h_{6} - \frac{v_6^2}{2 g}\) où \(\frac{v_6^2}{2 g}\) est la perte d'énergie cinétique à la sortie de l'aspirateur.
La différence d'énergie entre le point 5 et le point 6 est la perte de charge, transposable précédemment noté \(g h_{s56}\). Ce qui fait que la différence d'énergie entre les points 5 et 6' est la perte de l'aspirateur \(h_{faspi}\).
\(h_5=h_{6'}+h_{faspi}=h_{atm}+z_7+h_{faspi}\)
De plus à la sortie de la roue, selon Bernoulli, l'énergie locale en \(5\) s'exprime :
\(h_{5}= z_{5}+\frac{p_{5}}{\rho g}+\frac{v_5^2}{2 g}\)
Donc :
\(h_5=z_{5}+\frac{p_{5}}{\rho g}+\frac{v_5^2}{2 g}=h_{atm}+z_7+h_{faspi}\)
On sait que par définition \(h_s=z_5-z_7\).
Posons le point de fonctionnement au sigma critique alors la pressions absolue en \(5\) est égale à la tension de vapeur \(\frac{p_{5}}{\rho g}=h_v\)
On peut donc écrire :
\(h_s+h_v+\frac{v_5^2}{2 g} = h_{atm}+h_{faspi}\)
En isolant le terme de vitesse sous la roue on trouve :
\(\frac{v_5^2}{2 g}=h_{atm}+h_{faspi}-h_s+h_v\)
Et on observe que le second terme de l'équation est la définition du NPSH. Comme ceci est vrai pour le sigma critique :
\(\frac{v_5^2}{2 g} =NPSH_c=\sigma_c*H\)
Donc pour un fonctionnement en cavitation au sigma critique on obtient une relation entre la vitesse de l'écoulement en \(5\) et la hauteur de sustentation. Ce qui nous permet de conclure que pour un débit donné au sigma critique, la hauteur de sustentation est directement liée au diamètre de sortie de la roue.
Cette remarque a des conséquences majeures sur le dimensionnement de la turbine puisque ainsi pour un débit souhaité, le diamètre de la roue et son enfoncement sont liés.
Pour les différents usages on peut exprimer cette équation dans chaque système de similitude et trouver un chiffre limite ou la cavitation est établie sur toute la sortie de la roue.
Pour le système \(n_{11}-Q_{11}\) :
\(\frac{v_5^2}{2g}=\frac{8{Q_{11}}^2}{g\pi^2}H\)
\(\sigma_c=\frac{8Q_{11}^2}{g\pi^2} \rightarrow k_{11c}=\frac{\sigma_c}{Q_{11}^2}=\frac{8}{g\pi^2}=0,0826\)
\(k_{11c}=0,0826\)
Pour le système \(n_{ed}-Q_{ed}\) :
\(\frac{v_5^2}{2g}=\frac{8{Q_{ed}}^2}{\pi^2}H\)
\(\sigma_c=\frac{8Q_{ed}^2}{\pi^2} \rightarrow k_{edc}=\frac{\sigma_c}{Q_{ed}^2}=\frac{8}{\pi^2}=0,8106\)
\(k_{edc}=0,8106\)
Pour le système \(\varphi - \psi\) :
\(\frac{v_5^2}{2g}=\frac{\varphi^2\omega^2D^2}{8g}=\frac{\varphi^2U^2}{2g}=\frac{\varphi^2H}{\psi}\)
\(\sigma_c=\frac{\varphi^2}{\psi}\rightarrow k_{\varphi\psi c}=\kappa_c=\frac{\sigma}{{\varphi^2}/{\psi}}=1\)
\(\color{red}\kappa_c=1\)
Ces équations ont été développées pour le point de fonctionnement critique mais plus généralement, il y a une relation entre le débit et le nombre de cavitation au sigma d'installation de la turbine nommé sigma plant en anglais.
Fondamental :
De ce développement, on s'aperçoit donc que pour une turbine d'une dimension donnée, le débit et l'enfoncement sont liés à la cavitation. Il existe une limite théorique de hauteur de sustentation \(h_s\) sous laquelle, pour une débit donné, la cavitation isolera la roue du niveau aval et ainsi limitera la puissance de la machine.
Cette limite théorique s'exprime plus commodément par la variable \(k_c\) présentée ici sous les trois systèmes de similitudes.
Cette valeur de \(k_c\) est un minimum absolu et prend une importance fondamentale dans le dimensionnement des turbines.
En réalité, on n'implante jamais une machine à cette limite. En préconisant l'apparition de bulle comme un critère limite d'implantation d'une machine, on observe que le facteur \(k\) où les bulles apparaissent est plus grand que celui calculé ici. Comme explication, on peut imaginer que les aubes dont l'épaisseur n'est pas nulle réduisent la section de passage et voient des vitesses locales supérieures à \(v_5\) ce qui provoque l'apparition de la cavitation plus tôt. Le facteur k s'exprime comme étant le ratio du sigma observation de bulles sur le sigma critique calculé théoriquement. Seul le sigma observation est expérimental, le sigma critique lui est calculé.
\(k=\frac{\sigma_{apparition de bulles}}{\sigma_c}\)
Le facteur \(k\) devient donc un indice de la qualité du tracé hydraulique de la turbine. Plus il est petit, plus le tracé tolère un grand débit avant de caviter. Il devient le critère de dimensionnement pour un tracé donné.
En 2022, de très bons et très rares tracés peuvent montrer un \(k_{11}\) avoisinant 0,12 pour le sigma apparition de bulle. C'est une valeur qui s'est améliorée au fil du temps. Dans les années 80, 0,165 était un objectif valable.
Plus généralement, soit pour le système \(\varphi - \psi\), ces valeurs présentent des facteurs respectifs \(\kappa\) de 1,45 et 2 fois le sigma critique calculé lui pour un \(\kappa_c=1\). C'est à dire que le sigma apparition de bulles est \(\kappa\) (variant de 1,45 à 2) fois le sigma critique calculé.