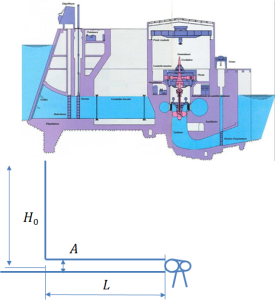
Calcul d'un transitoire sur un groupe turbine alternateur avec la méthode d'Allievi
Méthode : Méthode d'Allievi pour une fermeture progressive à partir d'une ouverture spécifiée
Dans un premier temps, cette méthode simule une fermeture progressive par une succession de fermetures partielles instantanées et généralise ainsi le calcul fait par l'équation de Joukowski à tout type de fermeture. Le premier extrant de ce calcul, c'est la surpression à la turbine et on verra dans un second temps l’interaction étroite entre le groupe turbine alternateur et le système hydraulique.
On observe que la méthode exposée ne tient pas compte des pertes de charge dans la conduite. Cette conduite doit être simple et non ramifiée et hypothétiquement considérée horizontale.
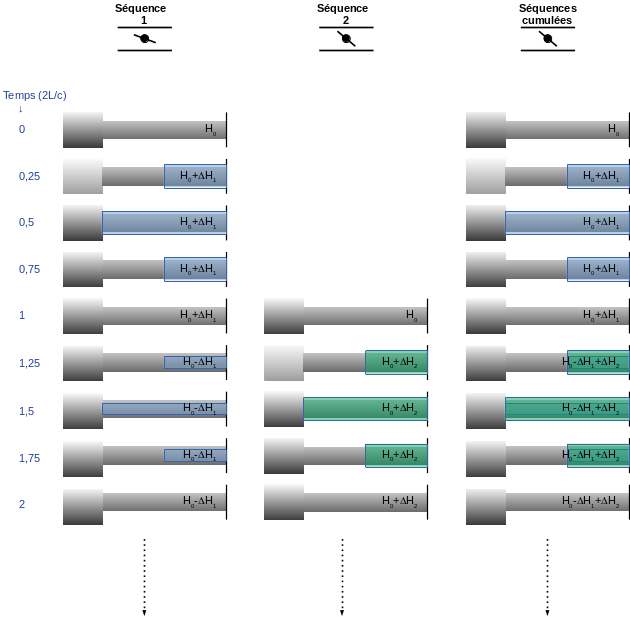
Pour un intervalle de temps entre 𝑡𝑖 et 𝑡𝑖+1 égal à 2𝐿/𝑐 et une vitesse d'écoulement passant de 𝑣𝑖 à 𝑣𝑖+1 instantanément, l'obturateur bouge instantanément, on observera la pression à l'obturateur évoluer ainsi :
Au temps initial \(t_0\)
\(H_0=H_0\)
Au temps suivant \(t_1=2L/c\)
\(H_1=H_0+\Delta H_1\)
À \(t_2=4L/c\)
\(H_2=H_0-\Delta H_1 +\Delta H_2\)
À \(t_3=6L/c\)
\(H_3=H_0+\Delta H_1 -\Delta H_2 +\Delta H_3\)
en généralisant pour des pas de temps de \(2L/c\)
\(H_i=\Delta H_i +2H_0 -H_{i-1}\)
et donc :
Cette dernière formulation s'applique à un pas de temps entier égal à \(2L/c\) .
Il peut être souhaitable, par exemple lorsque la variation de la vitesse de l'écoulement est importante, d'étudier plus finement le phénomène en diminuant le pas de temps.
Cette généralisation de la méthode d'Allievi se trouve ici.
Interaction dynamique du réseau hydraulique et de l'alternateur
L'adaptation de la méthode d'Allievi pour calculer les transitoires d'un groupe turbine-alternateur nécessite de saisir les interactions entre la turbine et l'alternateur en intégrant les variables qui influencent l'intrant principal de la méthode d'Allievi soit la variation de la vitesse de l'écoulement.
Il faut réaliser que dans un système hydraulique comportant un groupe turbine alternateur, la vitesse de l'écoulement dépend du point de fonctionnement de la turbine et donc de :
la configuration géométrique de la turbine soit : l'ouverture des directrices et celle des pales lorsqu'il s'agit d'une roue Kaplan,
l'énergie ou la chute disponible, la surpression obtenue lors du transitoire contribue à modifier cette énergie,
la vitesse de rotation du groupe ; en fonction des couples moteur et de freinage et de l'inertie en rotation du groupe, cette vitesse change.
Il y a plusieurs scénarios possibles pour obtenir un transitoire, observons deux cas fréquents : l'arrêt normal et le délestage.
Arrêt normal
L'alternateur maintient la vitesse synchrone durant tout le processus : la vitesse de rotation est donc constante.
Le distributeur est fermé à un taux programmé.
Le débit dépend du point de fonctionnement sur la colline c'est-à-dire:
L'ouverture des directrices à l'instant considéré.
Le n11, donc la vitesse de rotation synchrone et la chute (ou énergie) à cet instant.
La variation du débit provoque une variation inverse de la chute ce qui déplace le point de fonctionnement sur la colline. Dans une moindre mesure, le rendement de la turbine est aussi affecté.
Délestage
Le groupe en fonctionnement à la vitesse synchrone subit soudainement la déconnexion de l'alternateur du réseau qui dès lors n'absorbe plus l'énergie mécanique. La vitesse de rotation se met à augmenter.
L'inertie mécanique restreint l'accélération due au couple moteur de la turbine.
Le régulateur de vitesse ordonne au distributeur de fermer à un taux programmé.
Le débit dépend du point de fonctionnement sur la colline c'est-à-dire:
L'ouverture des directrices à l'instant considéré.
Le n11, donc de la vitesse de rotation et de la chute à cet instant.
La variation du débit provoque une variation inverse de la chute ce qui déplace le point de fonctionnement sur la colline. Dans une moindre mesure, la vitesse de rotation est aussi affectée de même que le rendement de la turbine qui permet de déterminer le couple moteur.
À partir de conditions initiales et pour chaque pas de temps \(2L/c\), on calcule:
Conditions initiales:
Ouverture des directrice
Débit
Chute
Vitesse de rotation
Calcul du couple moteur et du couple de freinage.
Calcul de la nouvelle vitesse de rotation
Calcul du nouveau débit
Calcul de la nouvelle chute
Pour chaque point de fonctionnement, le calcul de la chute et de la vitesse de rotation est un processus itératif. En effet, la variation de l'ouverture du distributeur cause une variation de vitesse qui crée une variation de la pression qui elle même influence la vitesse de l'écoulement. Aussi, la vitesse de rotation augmente ce qui déplace le point de fonctionnement sur la colline et donc le débit ce qui aussi fait varier la pression.
Méthode : Boucle de calcul d'un transitoire
Au temps 0, on a les conditions initiales: \(H_0\), \(Q_0\), \(\gamma_0\), \(n_0\), \(C_{m0}\) et \(C_{r0}\) soit la chute, le débit, l'ouverture des directrices, la vitesse de rotation, le couple moteur et le couple résistif.
Au temps 1 égal à \(2L/c\) :
On détermine 𝛾1, donc si on a une fermeture linéaire en \(T_{total}\) secondes:
\(\gamma_1=\gamma_0-\gamma_0*t_1/T_{total}\)
Le \(n_{11}\) du point de fonctionnement est calculé à partir de la chute supposée \(H_{sup1}\) et de la vitesse de rotation supposée \(n_{sup1}\) .
Sur la colline de rendement :
On détermine, à l'intersection du \(n_{11}\) et de l'ouverture \(\gamma_1\), le nouveau \(Q_{11}\) et le rendement à ce point de fonctionnement.
Le débit \(Q_1\) et la vitesse de l'eau \(v_1\) dans la conduite peuvent être alors calculés.
Calcul de la nouvelle chute nette \(H_1\) avec Allievi:
Il faut que \(H_{sup1}\) soit égal à \(H_1\). On doit donc itérer jusqu'à satisfaction.
De cette nouvelle chute, on peut calculer une nouvelle puissance \(P_1\), puis un nouveau couple moteur \(C_{m1}\) :
On détermine le couple de freinage \(C_{r1}\),
s'il s'agit d'une fermeture normale il est égal au couple moteur et donc la vitesse de rotation reste synchrone,
S'il s'agit d'un délestage, il est nul et il faut calculer une nouvelle vitesse de rotation en tpm:
On est ainsi capable de calculer un nouveau \(n_{11}\) à partir de la vitesse \(n_1\) et de la chute \(H_1\). Il faut toutefois que \(n_{sup}\) soit égale à \(n_1\) . On doit donc itérer jusqu'à satisfaction.
Les deux boucles d'itérations celle sur la chute et celle sur la vitesse doivent être répétées jusqu'à ce que les écarts entre les valeurs supposées et celles obtenues soient négligeables.
On répète cette boucle pour les temps suivants jusqu'à la fin du transitoire en remplaçant les indices 0 et 1 par \(i-1\) et \(i\) (sauf pour \(2H_0\) de l'équation d'Allievi qui reste contant pour tous les pas de temps).
Exemple : Calcul d'un transitoire du au délestage d'une turbine
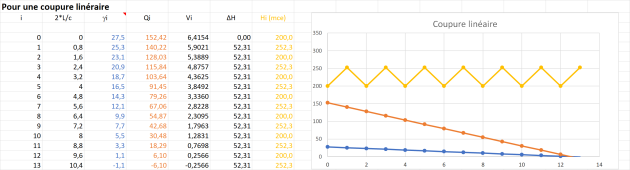
Pour cet exemple, on va calculer dans un premier temps, une coupure linéaire du débit.
D'abord, le pic de Michaud
Puis ce que donne la méthode d'Alievi pour une coupure linéaire :
Maintenant en simulant une coupure de débit causée par la fermeture des directrices déclenchée par un délestage :
Remarque : Conclusion sur Allievi et le pic de Michaud
En terme de surpression maximale, le pic de Michaud semble être une bonne évaluation et ne nécessite que peu de ressource. Par contre, pour comprendre le comportement du groupe et les chargements auxquels il est soumis et en particulier sa vitesse de rotation, la méthode d'Allievi est très utile. Il faut noter que dans l'exemple montré, les pertes par friction ne sont pas tenue en compte.
On trouvera une description de la méthode de calcul plus détaillée ici.