Méthode d'Allievi - généralisation pour pas de temps réduit [Turbines hydrauliques

Méthode d'Allievi - généralisation pour pas de temps réduit

Complément : Pas de temps demi de 2L/c

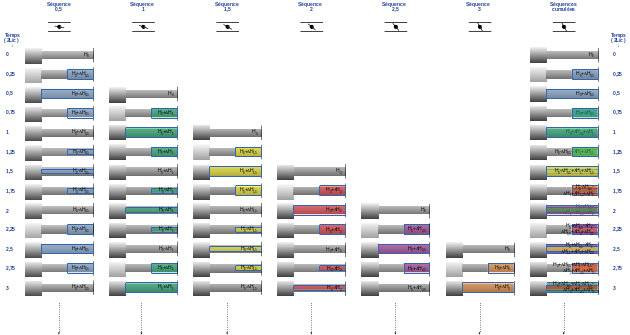
De façon similaire, si à tous les pas de temps L/c, l'obturateur bouge instantanément, on suivra plus finement le mouvement de l'obturateur et on obtiendra :

Effet de la coupure partielle instantanée et résultat cumulatif pour pas de temps 0.5 de 2L/c | Informations^[1]

Calcul de la pression à l'obturateur à chaque pas de temps (demi de $2L/c$)
Pas de temps	Pression à l'obturateur en mce
$t_0=0$	$H_0=H_0$
$t_{0,5}=L/c$	$H_{0,5}=H_0+\Delta H_{0,5}$
$t_1=2L/c$	$H_1=H_0+\Delta H_{0,5}+\Delta H_1$
$t_{1,5}=3L/c$	$H_{1,5}=H_0-\Delta H_{0,5}+\Delta H_1+\Delta H_{1,5}$
$t_2=4L/c$	$H_{2}=H_0-\Delta H_{0,5}-\Delta H_1+\Delta H_{1,5}+\Delta H_2$
$t_{2,5}=5L/c$	$H_{2,5}=H_0+\Delta H_{0,5}-\Delta H_1-\Delta H_{1,5}+\Delta H_2+\Delta H{2,5}$
$t_{3}=6L/c$	$H_{3}=H_0+\Delta H_{0,5}+\Delta H_1-\Delta H_{1,5}-\Delta H_2+\Delta H_{2,5}+\Delta H_3$
...	...

En posant :

$h_1=\Delta H_{0,5}+ \Delta H_1$

$h_2=\Delta H_{1,5}+ \Delta H_2$

$h_3=\Delta H_{2,5}+ \Delta H_3$

et ainsi de suite

$h_{0,5}=\Delta H_{0,5}$

$h_{1,5}=\Delta H_1 + \Delta H_{1,5}$

$h_{2,5}=\Delta H_2 + \Delta H_{2,5}$

$h_{3,5}=\Delta H_3 + \Delta H_{3,5}$

et ainsi de suite.

En généralisant pour des pas de temps de $L/c$ indice entier :

$H_{1}=H_0+h_{1}$

$H_{11}=H_0-h_{1}+h_{2}$

$H_{3}=H_0+h_{1}-h_{2}+h_{3}$

et ainsi de suite

$H_i=2 H_0 - H_{i-1}+ h_i$

En généralisant pour des pas de temps de $L/c$ indice demi :

$H_{0,5}=H_0+h_{0,5}$

$H_{1,5}=H_0-h_{0,5}+h_{1,5}$

$H_{2,5}=H_0+h_{0,5}-h_{1,5}+h_{2,5}$

$H_{3,5}=H_0-h_{0,5}+h_{1,5}-h_{2,5}+h_{3,5}$

et ainsi de suite

$H_i=2 H_0 - H_{i-1}+ h_i$

et donc :

$\color{red}H_i=2H_0 -\Delta H_{i-1}+\Delta H_{i-0,5}+\Delta H_i$

Complément : Pas de temps quart de 2L/c

Similairement ...

Calcul de la pression à l'obturateur à chaque pas de temps (quart de $2L/c$)
Pas de temps	Pression à l'obturateur en mce
$t_0=0$	$H_0=H_0$
$t_{0,25}=0,5L/c$	$H_{0,25}=H_0+\Delta H_{0,25}$
$t_{0,5}=L/c$	$H_{0,5}=H_0+\Delta H_{0,25}+\Delta H_{0,5}$
$t_{0,75}=1,5L/c$	$H_{0,75}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}$
$t_1=2L/c$	$H_{1}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_1$
$t_{1,25}=2,5L/c$	$H_{1,25}=H_0-\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_1+\Delta H_{1,25}$
$t_{1,5}=3L/c$	$H_{1,5}=H_0-\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}$
$t_{1,75}=3,5L/c$	$H_{1,75}=H_0-\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}+\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}$
$t_{2}=4L/c$	$H_{2}=H_0-\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}$
$t_{2,25}=4,5L/c$	$H_{2,25}=H_0+\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}$
$t_{2,5}=5L/c$	$H_{2,5}=H_0+\Delta H_{0,25}+\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}$
$t_{2,75}=5,5L/c$	$H_{2,75}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}-\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}+\Delta H_{2,75}$
$t_{3}=6L/c$	$H_{3}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}-\Delta H_{1,75}-\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}+\Delta H_{2,75}+\Delta H_{3}$
...	...

Posons :

$h_1=\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_{1}$

$h_2=\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}$

$h_3=\Delta H_{2,25}+\Delta H_{2,5}+\Delta H_{2,75}+\Delta H_{3}$

et ainsi de suite

$h_{0,25}=\Delta H_{0,25}$

$h_{1,25}=\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_1+\Delta H_{1,25}$

$h_{2,25}=\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}$

$h_{3,25}= \Delta H_{2,5}+\Delta H_{2,75}+\Delta H_{3}+\Delta H_{3,25}$

et ainsi de suite et similairement pour $h_{0,5}$ et $h_{0,75}$.

En généralisant pour les pas de temps $L/c$ indice quart :

$H_{0,25}= H_0+h_{0,25}$

$H_{1,25}=H_0-h_{0,5}+h_{1,25}$

$H_{2,25}=H_0+h_{0,25}-h_{1,25}+h_{2,25}$

$H_{3,5}=H_0-h_{0,25}+h_{1,25}-h_{2,25}+h_{3,5}$

et ainsi de suite.

$H_i=2 H_0 - H_{i-1}+ h_i$

et donc :

$\color{red}H_i=2H_0 -\Delta H_{i-1}+\Delta H_{i-0,75}+\Delta H_{i-0,5}+\Delta H_{i-0,25}+\Delta H_i$

Méthode d'Allievi - généralisation pour tout pas de temps

Fondamental :

Pour $m$ un entier positif, le pas de temps en unité de $2L/c$ s'exprime comme :

$j=2^{-m}$

et donc m est égal à 0, 1, 2 ...

$j$ prend les valeurs 1, 0,5 , 0,25 ...

Le nombre de fraction de pas

$n=1/j$

et prends les valeurs 1, 2, 4 ...

Suivant la nomenclature utilisée précédemment :

$\begin{matrix} h_{i} = \sum_{k = 1}^{k = n} Δ H_{i-kj+j} \\ H_{i} = 2 H_{0} - H_{i-1} + h_{i} \end{matrix}$

Pas de temps	Pression à l'obturateur en mce
\(t_0=0\)	\(H_0=H_0\)
\(t_{0,5}=L/c\)	\(H_{0,5}=H_0+\Delta H_{0,5}\)
\(t_1=2L/c\)	\(H_1=H_0+\Delta H_{0,5}+\Delta H_1\)
\(t_{1,5}=3L/c\)	\(H_{1,5}=H_0-\Delta H_{0,5}+\Delta H_1+\Delta H_{1,5}\)
\(t_2=4L/c\)	\(H_{2}=H_0-\Delta H_{0,5}-\Delta H_1+\Delta H_{1,5}+\Delta H_2\)
\(t_{2,5}=5L/c\)	\(H_{2,5}=H_0+\Delta H_{0,5}-\Delta H_1-\Delta H_{1,5}+\Delta H_2+\Delta H{2,5}\)
\(t_{3}=6L/c\)	\(H_{3}=H_0+\Delta H_{0,5}+\Delta H_1-\Delta H_{1,5}-\Delta H_2+\Delta H_{2,5}+\Delta H_3\)
...	...

Pas de temps	Pression à l'obturateur en mce
\(t_0=0\)	\(H_0=H_0\)
\(t_{0,25}=0,5L/c\)	\(H_{0,25}=H_0+\Delta H_{0,25}\)
\(t_{0,5}=L/c\)	\(H_{0,5}=H_0+\Delta H_{0,25}+\Delta H_{0,5}\)
\(t_{0,75}=1,5L/c\)	\(H_{0,75}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}\)
\(t_1=2L/c\)	\(H_{1}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_1\)
\(t_{1,25}=2,5L/c\)	\(H_{1,25}=H_0-\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_1+\Delta H_{1,25}\)
\(t_{1,5}=3L/c\)	\(H_{1,5}=H_0-\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}\)
\(t_{1,75}=3,5L/c\)	\(H_{1,75}=H_0-\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}+\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}\)
\(t_{2}=4L/c\)	\(H_{2}=H_0-\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}+\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}\)
\(t_{2,25}=4,5L/c\)	\(H_{2,25}=H_0+\Delta H_{0,25}-\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}+\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}\)
\(t_{2,5}=5L/c\)	\(H_{2,5}=H_0+\Delta H_{0,25}+\Delta H_{0,5}-\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}+\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}\)
\(t_{2,75}=5,5L/c\)	\(H_{2,75}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}-\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}-\Delta H_{1,75}+\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}+\Delta H_{2,75}\)
\(t_{3}=6L/c\)	\(H_{3}=H_0+\Delta H_{0,25}+\Delta H_{0,5}+\Delta H_{0,75}+\Delta H_{1}-\Delta H_{1,25}-\Delta H_{1,5}-\Delta H_{1,75}-\Delta H_{2}+\Delta H_{2,25}+\Delta H_{2,5}+\Delta H_{2,75}+\Delta H_{3}\)
...	...