Cavitation et vitesse spécifique
Fondamental : La cavitation au point critique et la vitesse spécifique
On peut constater que la définition de la vitesse spécifique, par exemple dans le système de l'EPFL, est :
\(\nu=\frac{\varphi^{0,5}}{\psi^{0,75}}\)
alors que, comme on vient de le voir, le sigma critique suit une loi très similaire :
\(\sigma_c=\frac{\varphi^2}{\psi}\).
Ces deux formulations suivent la même tendance : quand la vitesse spécifique croît le nombre de cavitation croît aussi, et inversement.
On peut donc en conclure que les turbines de faible vitesse spécifique ont un meilleur comportement en cavitation que les turbines de plus haute vitesse spécifique.
Des deux équations précédentes, on obtient la relation :
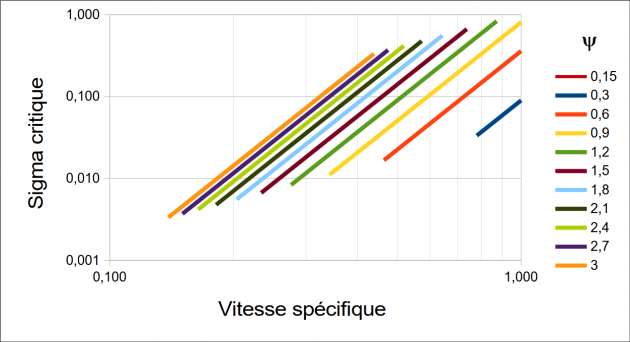
\(\sigma_c=\nu^4\psi^2\)
Qu'on illustre dans le graphique log-log suivant :
C'est ce qui est exprimé aussi par les graphiques qui montrent l'évolution du type de turbine avec la vitesse spécifique. Voir à ce sujet Les types de turbine hydraulique.
Remarque :
On observe que sur le graphique précédent, il n'y a pas de correspondance directe entre la vitesse spécifique et le sigma critique. En fait, pour y arriver, il faut déterminer la vitesse de rotation qui permet alors d'associer une vitesse spécifique à un sigma critique.
Fondamental : Le sigma d'implantation et la vitesse spécifique
On a vu dans le chapitre précédent intitulé La cavitation et Bernoulli que le sigma d'implantation \(\sigma_p\) est lié au sigma critique \(\sigma_c\) par le facteur \(\kappa\) de la façon suivante :
\(\sigma_p=\kappa \sigma_c\)
La valeur de \(\kappa\) varie selon la qualité du tracé entre 1,4 et 2 et même plus pour les machines anciennes.
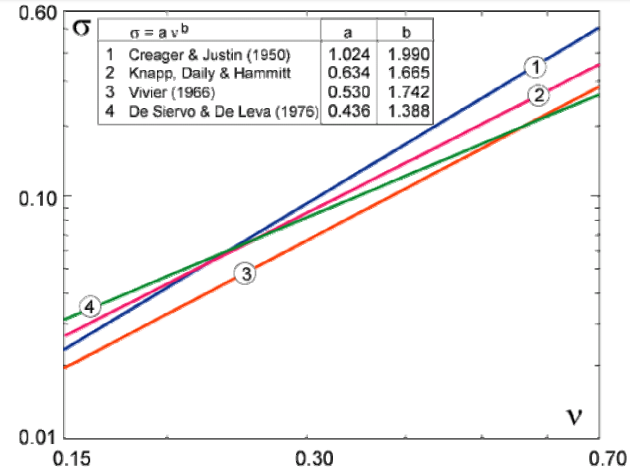
À ce sujet des statistiques ont été compilées par différents auteurs à différentes époques et sont présentées dans le graphique suivant :
Exemple : Calcul statistique d'un sigma d'implantation pour une turbine
Soit une turbine présentant une vitesse spécifique à la pleine charge de \(\nu=0,22\) sous un coefficient d'énergie \(\psi=3,06\).
\(\sigma_c=\nu^4\psi^2=0,22^4*3,06^2= 0,022\)
Si on compare ce résultat avec les courbes statistiques données au graphique précédent. On obtient pour chacune des références un sigma d'implantation \(\sigma_p\) et la valeur \(\kappa\) y correspondant.
\(\nu=0,22\) | \(\sigma_c=0,022\) | |||
Ref. | a | b | \(\sigma_p=a\nu^b\) | \(\kappa= \sigma_p/\sigma_c\) |
1 | 1,024 | 1,99 | 0,050 | 2,287 |
2 | 0,634 | 1,665 | 0,051 | 2,316 |
3 | 0,53 | 1,742 | 0,038 | 1,723 |
4 | 0,436 | 1,388 | 0,053 | 2,423 |
On s'aperçoit la référence 3 semble assez optimiste pour sa période de publication.
Cette turbine citée en exemple est en fait celle de Churchill Falls conçue autour de 1970 pour une mise en service complète en 1976. Son sigma d'implantation est de \(\sigma_p=0,049\) pour un \(\kappa=2,28\).
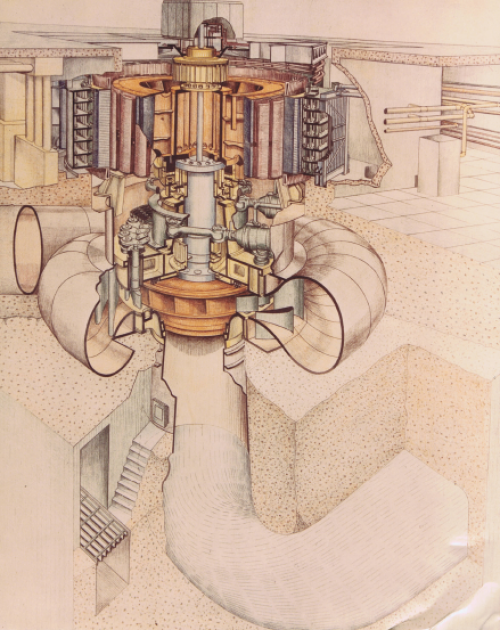
Si on projette une éventuelle réhabilitation de cette turbine, si on utilise une valeur plus moderne de \(\kappa_r=1,8\) en conservant la chute, la vitesse de rotation et le rendement, on peut écrire, pour la machine existante avec l'indice 0 et la machine réhabilitée l'indice r :
\(\sigma_{p0} = \kappa_0 \frac{\varphi_{p0}^2}{\psi}\)
\(\sigma_{pr} = \kappa_r \frac{\varphi_{pr}^2}{\psi}\)
Puisque le sigma d'installation est le même pour les deux cas :
\(\frac{\varphi_{pr}}{\varphi_{p0}}=\sqrt{\frac{\kappa_0}{\kappa_r}}\)
Ainsi, en conservant le diamètre de la roue et tous les facteurs ci-haut mentionnés, on peut augmenter le débit et donc la puissance de :
\(\sqrt{\frac{\kappa_0}{\kappa_r}}=\sqrt{ \frac{2,28}{1,8}}=1,12\ \).
Ce 12% d'augmentation de puissance s'appuie sur l'amélioration de la science hydraulique depuis 50 ans.